|
|
|
\require{AMSmath}



Reuzenrad
Goedenavond,
Mijn vraag betreft het volgende: Vanaf tijdstip t = 0 draait een reuzenrad met constante snelheid rond.Vanaf dit tijdstip wordt de hoogte vanaf de grond gemeten van stoeltje A gegeven door de formule:
H(t) = 21 +18.sin($\pi$:14)(t-4)
Schuitje B is ook getekend en ik kan zien dat de fasevoorsprong 6/16 is dus is de bijbehorende formule:
H(t) = 21 + 18.sin($\pi$/14)(t +6.5)
Nu is de vraag: bereken de tijdstippen waarop A en B op dezelfde hoogte zitten. Periode (0,42)
Ik dacht: de 2 vergelijkingen aan elkaar gelijkstellen en oplossen. Ik vind voor t=5,75.
Maar er zijn nog andere waarden volgens mijn GR nl. 19,75 en 33,75. Dit begrijp ik ook wel, maar hoe kan ik deze waarden, als oplossingen krijgen via 'de vergelijkingen aan elkaar gelijkstellen'?
Alvast bedankt.
Katrij
Leerling bovenbouw havo-vwo - zaterdag 12 juli 2008
Antwoord
Je moet bedenken dat er doorgaans oneindig veel oplossingen zijn van de vergelijking sin(a)=sin(b).

De toevoeging k·2$\pi$ staat er niet voor niets! Op 6. Vergelijkingen kan je er meer over vinden.
In jouw geval krijg je dan zoiets:
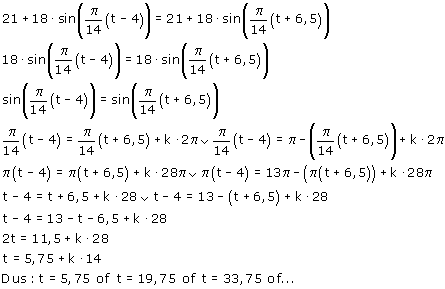
Hopelijk helpt dat.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 13 juli 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|