WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hypothesen toetsen en de TI83

DE OPDRACHT:
H0: medicijn werkt in minstens 90% van de gevallen
H2: medicijn werkt in minder dan 90% van de gevallen

Er wordt een onderzoek gedaan met 50 patiënten. Er wordt afgesproken dat het significantieniveau 0,05 moet zijn.

MIJN OPLOSSING:
α=0,05
n=50
p=0,9
E(X)=45

P(Xg|n=50 en p=0,9)0,05

we hoeven complementregel hier niet te gebruiken!!
want H1 zegt minder dan 90%

GR: Y1=binomcdf(50, 0,9 , X)
Y2=0,05
nu wil ik het snijpunt van deze twee functies gaan bepalen op de volgende manier:

window Xmin=35 Xmax=55
Ymin=0 Ymax=1 (kansen kunnen toch niet groter dan 1 en kleiner dan 0 zijn)

CALC/5:intersect
First curve? ik doe het sterretje op grafiek van Y1
Second curve? ik doe het sterretje op grafiek van Y2
Guess? ik probeer het sterretje zo goed mogelijk op het snijpunt van Y1 en Y2 te plaatsen

mijn GR geeft nu:
ERR:NO SIGN CHNG
1:Quit

MIJN VRAGEN:
Heb ik mijn window goed ingesteld?
wat betekent deze foutmelding precies?
Ik weet dat er andere manieren zijn om dit te bepalen met de GR, maar ik zou graag willen weten hoe ik dit WEL zou kunnen doen met het snijpunt van Y1 en Y2. Wat doe ik fout?

Ik heb trouwens een TI-83 van TEXAS INSTRUMENTS

alvast harstikke bedankt!!
anne z
Leerling bovenbouw havo-vwo - maandag 25 november 2002

Antwoord

Het probleem wordt duidelijk als je naar de tabel kijkt in plaats van naar een grafiek.
Met je snijpunt ben je op zoek wanneer P(Xg)=0.05.
Uit de onderstaande tabel lijkt dat te zijn tussen 40 en 41.

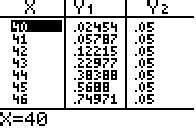
Als we de stapgrootte in de tabel verfijnen blijkt dat die kans nooit precies 0.05 wordt, zoals te zien is in de volgende tabel.

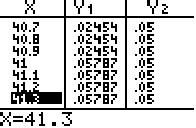
Wat hier aan de hand is, dat een binomiale verdeling een zgn. 'discrete' verdeling is. Het gaat over aantallen successen en het is niet mogelijk om 40.8 keer succes te hebben. Hoogstens 40.8 keer succes is hetzelfde als hoogstens 40 keer succes.
Ik zou je aanraden om bij dit soort opgaven de oplossing altijd uit de tabel te halen en niet uit de grafiek of met de Solver. Met de tabel kun je ook makkelijker je conclusie trekken:
Bij X=40 wel verwerpen
Bij X=41 niet verwerpen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 26 november 2002