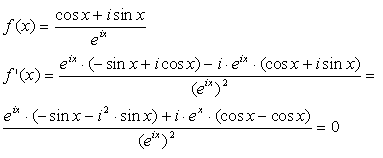WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Formule van Euler

Hey,

Graag zou ik het bewijs kennen van Euler's mooiste formule, namelijk e^i$\pi$+1 =0. Het zou echt handig zijn voor mijn eindwerk dat over transcendente getallen gaat. En e en $\pi$ zijn transcendente getallen.

Alvast bedankt
Jeroen
3de graad ASO - zaterdag 10 mei 2008

Antwoord

Beste Jeroen,
Oorspronkelijk bewees Euler deze mooie formule met behulp van Taylor reeks ontwikkeling.
Een misschien wat makkelijker bewijs is hetvolgende:
Stel je hebt de mogelijk complexe functie f(x), waarvan je de afgeleide bepaalt:

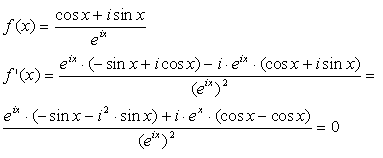
Daarbij is gebruik gemaakt van: i²=-1.
Je ziet dat de afgeleide altijd 0 is, dus de functie is constant.
Bereken f(0) en je ziet dat f(0)=1,en dus geldt altijd: f(x)=1, waaruit volgt:

e^ix=cosx+isinx.

Voor de laatste stap vul je in: x=$\pi$.

Groet, Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 19 mei 2008