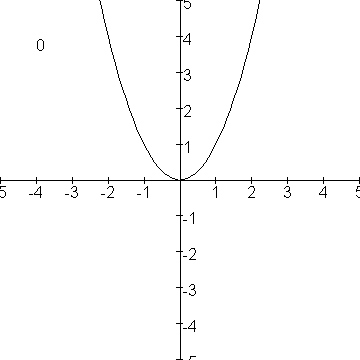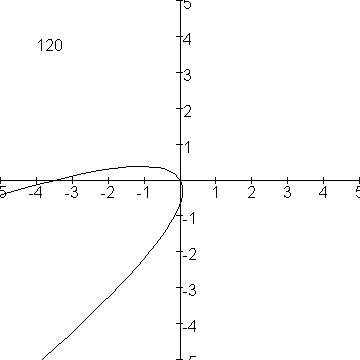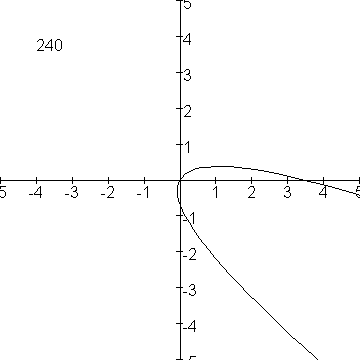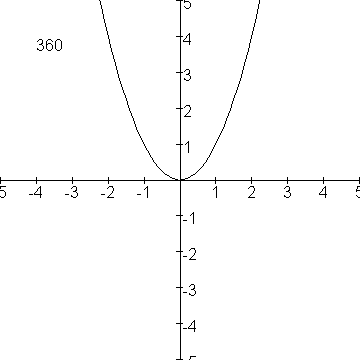WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Draaien van een paraboolfunctie

ik ben bezig met mijn profielwerkstuk, mijn onderwerp is het draaien van een paraboolfunctie, over een hoek a.
met behulp van de stelling van pythagoras waarin c de afstand is tussen de oorsprong en de plek waar de functie zich voor de desbetreffende T bevind(T is mijn variabele in de parametervoorstelling. x=T en y=T² c=(T⁴+T²)
ik had namelijk bedacht dat ze voor dezelfde T dezelfde, afstand tussen de oorsprong en het punt waar de functie zich op dat moment bevind moeten hebben.
vervolgens heb ik met SOS CAS TOA
bedacht wat de hoek moest zijn tussen 'lijnstuk' c en de y-as. (a+ tan (1/T)

ik kom tot de volgende parametervoorstelling:

x = (T⁴+T²) ·sin (a+ tan (1/T))
y = (T⁴+T²) ·cos (a+ tan (1/T))

als ik hem invoer in mijn rekenmachine krijg ik er echter niet de gewenste gedraaide parabool uit.

zit er een fout in mijn berekening? of heb ik iets over het hoofd gezien?
mvg, en de beste wensen voor 2008
niek
niek v
Leerling onderbouw vmbo-havo-vwo - woensdag 2 januari 2008

Antwoord

Veronderstel dat je de parabool
x=t
y=t²
over een hoek a om de oorsprong wil draaien, dan is de parametervoorstelling van de gedraaide parabool:
x=t·cos(a)-t²sin(a)
y=t·sin(a)+t²cos(a)

Voor achtereenvolgende waarden van a heb ik hier maar eens een plaatje van gemaakt:

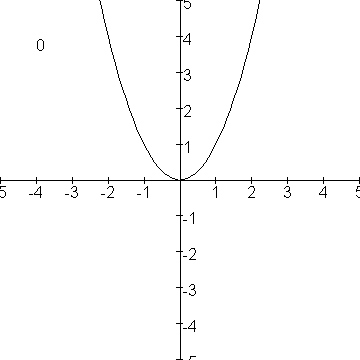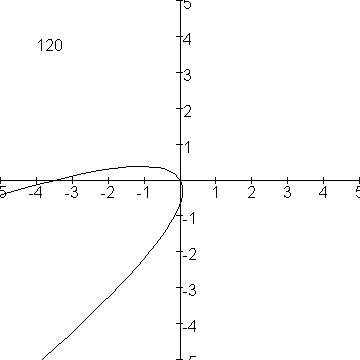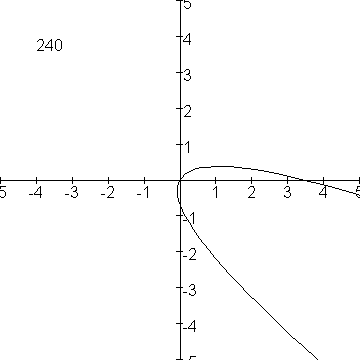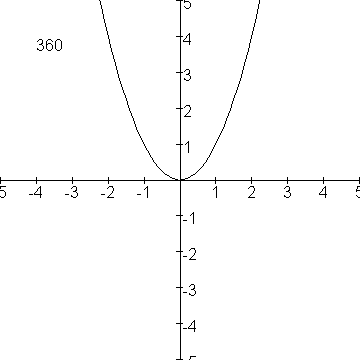
In het algemeen als je de grafiek van de parametervoorstelling
x=f(t)
y=g(t)
over een hoek a om de oorsprong wil draaien dan is de parametervoorstelling van de gedraaide grafiek:
x=f(t)·cos(a)-g(t)·sin(a)
y=f(t)·sin(a)+g(t)·cos(a).

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 januari 2008