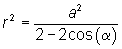WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Hoeken bepalen van ongelijkzijdige piramide met rechthoek als basis

Dit is een reactie op vraag 47188

Hallo Anneke,

Het betreft een regelmatige veelhoek. Hierbij een foto van het produkt wat we hebben gemaakt met je formule.

Het is een opvangtrechter onder een filter (op de foto staat ie op z'n kop). Het past perfect!

groet,

Marten
Marten
Student hbo - donderdag 2 november 2006

Antwoord

Dag Marten,

Voor een piramide met als grondvlak een regelmatige n-hoek met zijde a, en hoogte h, kun je de hoek tussen twee opstaande zijvlakken als volgt berekenen:
O is het centrum van de n-hoek. T is de top van de piramide.

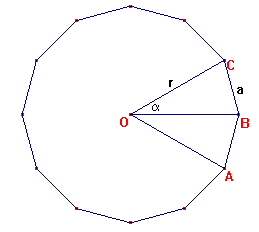
de hoek BOC is gelijk aan a=^2p/_n
Met behulp van de cosinusregel kun je de afstand r van O tot een hoekpunt (bijvoorbeeld A) uitdrukken in a:
a² = r² + r² - 2·r·r·cos(a), dus

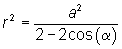
Leg nu een driedimensionaal assenstelsel aan met O als oorsprong, OB als x-as, de y-as in het grondvlak loodrecht op OB, en OT als z-as.
Je kunt dan van A, B, C en T de coördinaten uitdrukken in r en a.
Bijvoorbeeld: C = (r·cos(a), r·sin(a), 0)
Bepaal vervolgens de vectoren TA, TB en TC.
Met behulp van het uitproduct kun je hiermee de normaalvectoren van de zijvlakken TAB en TBC vinden.
De hoek tussen deze normaalvectoren is de gezochte hoek (of zijn supplement).
Lukt dit?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 3 november 2006

Re: Re: Re: Re: Hoeken bepalen van ongelijkzijdige piramide met rechthoek als b