|
|
|
\require{AMSmath}



Primitiveren van goniometrische functies
hallo. ik heb over enkele dagen een wiskunde proefwerk over integreren, differentieren én goniometrische functies.
nu ben ik op een vraag gestuit waar ik gewoon niet uit kom...
"Gegeven is de functie f(x)=1+cos(1/2X) met domein [0,2p]. Het vlakdeel V wordt begrensd door de assen en de grafiek van f.
bij de eerste deelvraag moest ik de oppervlakte van het vlakdeel V berekenen, en daar kwam ik goed uit (antwoord: 2p), maar bij de tweede deelvraag werd de grafiek van f om de x-as gewenteld en moest je vervolgens op hetzelfde domein de inhoud van het omwentelingslichaam berekenen...
hier volgt de berekening zover ik ben gekomen:
ò[0,2p] p·(f(X)2)dx
ò[0,2p] p·(1+cos(1/2X)2dx
ò[0,2p] p·(1+2cos(1/2X)+cos2(1/2X)dx
ò[0,2p] p+2pcos(1/2X)+pcos2(1/2X)dx
vervolgens moet je deze primitiveren, maar ik heb geen flauw idee hoe je een cos2X moet primitiveren, noch een sin2X...
zelfs als ik een fout gemaakt blijk te hebben, en je helemaal geen cos2X hoeft te primitiveren, zou ik toch erg graag willen weten hoe dit moet... 
alvast bedankt...
Carel
Leerling bovenbouw havo-vwo - zondag 15 oktober 2006
Antwoord
Met onderstaande formule kan je cos2() schrijven als cos() en dan lukt het wellicht beter...
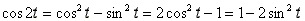
Zie Formulekaart

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 15 oktober 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|