WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kansbereken met een wegendiagram

Hoi,ik heb hier een vraag over theoretische kansen.
Een inwoner van stad X trekt elke werkdag met de wagen naar stad Z om zijn dagtaak te vervullen. Daarbij heeft hij de keuze tussen twee wegen (a en b) die hem ongeveer even snel naar de tussenliggende stad Y brengen. Vandaar neemt hij meestal de hoofdweg (d) naar Z. Bij grote drukte kan hij echter ook gebruik maken van twee alternatieve wegen (c en e). De keuze van het gevolgde traject hangt voor een deel af van de omstandigheden, maar de ervaring leert dat hij weg a driemaal meer benut dan weg b en dat hij weg d dubbel zo vaak gebruikt als weg c en ook dubbel zo vaak als weg e.
Nu is de vraag hoe groot de kans is dat de persoon:
1) het traject a-c volgt?
2) niet weg a en ook niet weg d neemt?

Voorstelling
x   ®    Y   ®              Z
      a            c
                 ®           
    ®          d 
      b          ®
                   e
weg a wordt driemaal meer benut als weg b (3)
weg d wordt dubbel zo vaak gebruikt als weg c (2)
weg d wordt ook dubbel zo vaak gebruikt als weg e (2)
weg e en c worden op hun beurt ook één keer gebruikt (1+1)

mijn oplossing:
1) 3+1+2+2+1+1 = 10
weg a wordt dan 3/10 gebruikt
weg b wordt 1/10 gebruikt
weg c, net als weg e wordt ook 1/10 gebruikt
en weg d wordt 4/10 gebruikt

traject a-c = 3/10 * 1/10= 3/10

2) dit is moeilijker en kan ik dus niet vinden

ik hoop dat jullie mij kunnen helpen
groetjes, nathalie

Nathal
3de graad ASO - zaterdag 27 mei 2006

Antwoord

Eerst maar 's een tekening:

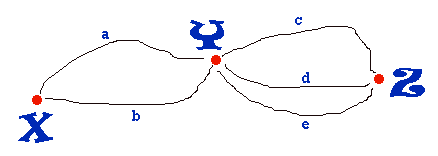
Nu is het verreweg het handigst om de zin 'De keuze van het gevolgde traject hangt voor een deel af van de omstandigheden, maar de ervaring leert dat hij weg a driemaal meer benut dan weg b en dat hij weg d dubbel zo vaak gebruikt als weg c en ook dubbel zo vaak als weg e.' te vertalen naar kansen.

Als je a driemaal meer benut dan b dan is de kans op a gelijk aan ³/₄ en de kans op b gelijk aan ¹/₄. Ze moeten samen natuurlijk wel 1 zijn. Hetzelfde geldt voor c, d en e. Op dezelfde manier levert dat:

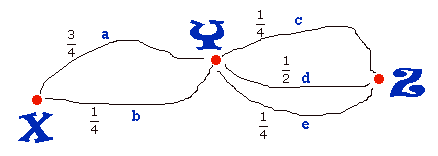
Je hebt dan het probleem helemaal in kaart gebracht en kan je 's gaan denken aan het beantwoorden van de vragen.

Wat is nu de kans dat hij a-c neemt? Deze kans is ³/₄·¹/₄=³/₁₆. Handig hè?

Dan moet je b. zelf maar 's proberen!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 27 mei 2006

Re: Kansbereken met een wegendiagram