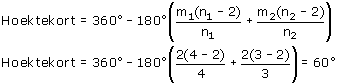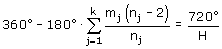WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Afleiden formule hoektekort

Dit is een reactie op vraag 31272

Owkee, ondertussen snap ik het bewijs al (alleen snap ik nog niet hoe jullie aan Zn=Hm=2R komen, maar daarover ging mijn vorige vraag al natuurlijk ...)
Nu ben ik echter op zoek naar ditzelfde bewijs voor halfregelmatige veelvlakken. Nu heb je namelijk een vaste n die voor alle zijvlakken hetzelfde is. Bij halfregelmatige veelvlakken is dit niet zoek.
Ik weet dat het hoektekort d gelijk is aan

360° - å_j=1^k[(n_j - 2) * 180° / n_j ]

Ik moet dus bewijzen dat dit gelijk is aan 720°/H, maar ik heb geen idee hoe ik de versie voor regelmatige veelvlakken die hier staat moet aanpassen zodat die ook geldt voor halfregelmatige veelvlakken.
Inge V
Student universiteit België - vrijdag 17 maart 2006

Antwoord

We nemen een voorbeeld!

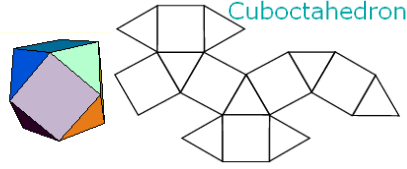
http://mathworld.wolfram.com/ArchimedeanSolid.html

Zijvlakken: 6 vierkanten en 8 driehoeken (48)
n₁=4 en m₁=2
n₂=3 en m₂=2
Hoekpunten: 12 hoekenpunten met 4 ribben (48)
Ribben: 24 ribben (48)

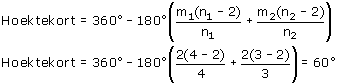
..en dat is gelijk aan 720°/12, dus dat is alvast wat...

Te bewijzen: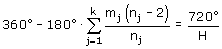

...maar dan?
Zie Op zoek naar halfregelmatige veelvlakken

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 24 maart 2006