|
|
|
\require{AMSmath}
Cosinusregel
Hallo,
Mijn vraag gaat over de cosinusregel.
Ik heb een scherpe driehoek ABC en een hoogtelijn vanuit C
met voetpunt D. (CD)=h
waarvan ad=x en bd =(c-x)
te bewijzen a2 = b2+ c2-2bccosalfa
a2=(c-x)2 + h2 =c2 - 2cx + x2 + h2
en b2= x2+ h2
dus a2+ b2-2cx waarbij x2+ h2 vervangen is door b2.
ik hoop dat ik dit goed begrijp.
Dat-2cx vervangen wordt door -2bccosalfa snap ik niet.
b·cosalfa = lengte x. snap ik.
hier kom ik niet verder.
BVD
Mari S
Ouder - zondag 29 januari 2006
Antwoord
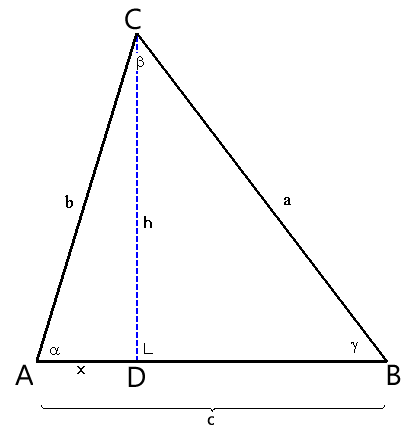
We stellen vast:
x=b·cosa
h=b·sina
x2+h2=
(b·cosa)2+(b·sina)2=
b2·cos2a+b2·sin2a=
b2(cos2a+sin2a)=
b2
-2cx=-2c·b·cosa=-2bc·cosa
Waarmee we volgens mij helemaal rond zijn...
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 29 januari 2006
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
