WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Maximum- en minimumvraagstukken

Is het mogelijk van de algemene werkwijze is uit te leggen en als het kan een voorbeeldje aub van extremavraagstukken.
Geertr
3de graad ASO - maandag 15 oktober 2001

Antwoord

Laten we eens naar een eenvoudig voorbeeld kijken:
f(x) = 2x² - 4x + 1
Met: D_f=[-2,3>

Stappen:
1. Bereken f(x) voor de randen.
2. Bepaal maxima/minima van f(x).

1.
f(-2)=17
f(3)=7

2.
Bepaal de afgeleide van f(x).
f'(x)=4x-4
Neem f'(x)=0
4x-4=0
4x=4
x=1
Teken het tekenverloop van de afgeleide.

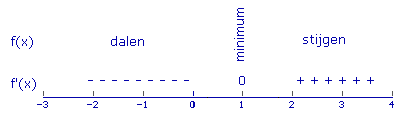
Bepaal de maxima en minima van f(x).
f(x) heeft een minimum bij x=1: f(1)=-1

Dus het minimum van f(x) op het gegeven domein is -1 en het maximum is 17.

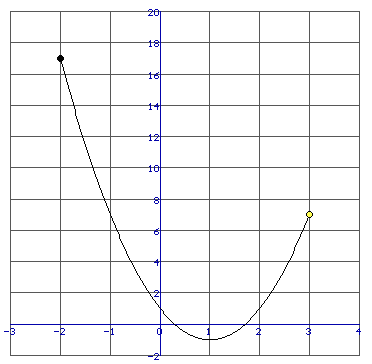
Uiteraard zijn er dan allerlei verschillende varianten mogelijk. Bijvoorbeeld dat het minimum of maximum gewoon tussen de randwaarden ligt... dat er sprake is van meerder maxima en minima, enz.

Voor een uitgewerkt voorbeeld op maat, kan je een nieuwe vraag stellen met de opgave erbij.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 15 oktober 2001