|
|
|
\require{AMSmath}
Extremum probleem : een kubus in een piramide
Hallo
Er is een vraag in de database die er op lijkt maar deze is toch nog iets anders... Ik geraak er maar niet uit.
Een kubus met een volume van 64 cm3 is ingeschreven in een regelmatige vierzijdige piramide.- Bepaal de hoogte van de piramide met
het kleinste volume. - Bepaal het overeenkomstige volume.
Dank bij voorbaat! Mvg.
Geloen
Student Hoger Onderwijs België - maandag 28 februari 2005
Antwoord
Eerst maar eens een tekening:
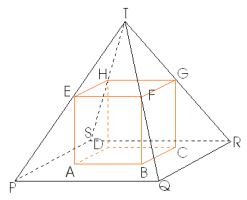
Kijken we naar het vooraanzicht dan zien we dit:
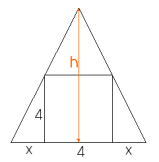
Ik noem het 'stuk dat uitsteekt' maar even 'x'. De hoogte van de piramide noem ik h. Je kunt dan h uitdrukken in x. Je maakt daarbij gebruik van gelijkvormigheid.
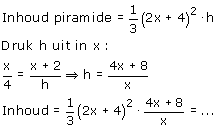
Je kunt de uitdrukking vereenvoudigen en vervolgens het minimum bepalen. Uiteraard kan dat met de afgeleide, tekenverloop... enz...
Ik heb even de grafiek getekend en dat ziet er in ieder geval veelbelovend uit:
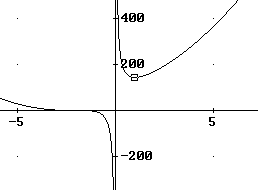
Hopelijk lukt het zo verder...
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 28 februari 2005
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
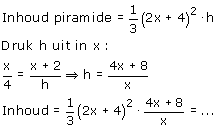
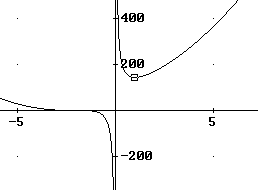
Re: Extremum probleem : een kubus in een piramide