|
|
|
\require{AMSmath}



Stabiele en instabiele dekpunten zoeken
Hallo
Van f(x)=x2-(1/4), zou ik graag de dekpunten vinden...
Ik loste de vergelijking (x2-(1/4)=x) op en vond: (1Ī÷2)/2.
Maar als ik met de rekenmachine iteraties uitvoer met omliggende punten kom ik steeds -0,5 en 0,5 uit (Na herhaaldelijk itereren...)
Wat is nu het stabiel en wat het instabiel dekpunt?
Of zijn -0,5 en 0,5 de twee stabiele dekpunten?
Miguel
Student Hoger Onderwijs BelgiŽ - donderdag 20 januari 2005
Antwoord
Hoe je op -0,5 en 0,5 uit kunt komen is me een raadsel.
Kijk maar in onderstaande webgrafiek:
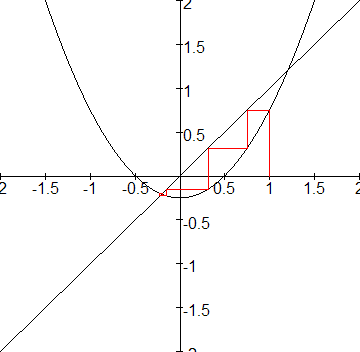
Het instabiele dekpunt is(1+÷2)/2.
Het stabiele dekpunt is (1-÷2)/2.
Dit kun je ook berekenen door in beide dekpunten f '(x) uit te rekenen en na te gaan of |f '(x)| 1. 1.
|f '((1+÷2)/2)|=1+÷2 1 1
|f '((1-÷2)/2)|=|1-÷2| 1. 1.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 20 januari 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









 1.
1.  1
1 
