|
|
|
\require{AMSmath}



Ceva en een toepassing ervan
Hallo,
Ik heb een vraag over Ceva en zijn toepassing ervan.
Bekend is de stelling van Ceva in dit verband. De vraag luidt als volgt:
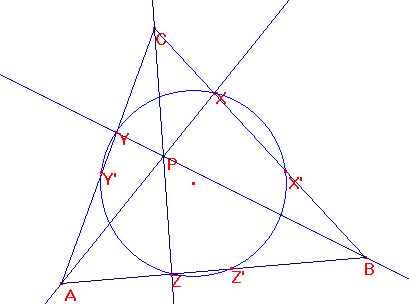
Teken een driehoek ABC en een punt P binnen die driehoek. De lijnen AP, BP en CP snijden de zijden BC, CA en AB in respectievelijk X, Y en Z.
Construeer de cirkel door X, Y en Z.
Deze cirkel snijdt de driehoek in nog drie andere punten, namelijk X' (op BC),Y' (op CA) en Z' (op AB). Teken de lijnen AX', BY' en CZ'.
Formuleer een vermoeden over deze drie lijnen en verander driehoek ABC of punt P om dit vermoeden te bevestigen.
Bewijs je vermoeden.
Nu kom ik wel al zelf een aardig eindje volgens mij met het gebruik van de stelling van de macht van een punt t.o.v. een cirkel (in ons geval bijvoorbeeld punt A t.o.v Y en Y'), maar ik krijg het bewijs niet sluitend en heb het gevoel dat er nog een belangrijk deel mist. Ik loop echt vast met het bewijzen dat die lijnen door één punt gaan.
Ik zou erg geholpen zijn als iemand me hier verder mee kan helpen.
M.v.g. Francis
Franci
Student hbo - vrijdag 4 juni 2004
Antwoord
Dag Francis,
Je zit inderdaad in de goede richting.
Je weet dat uit de stelling van Ceva volgt:

Nu is het enkel een kwestie van gelijke factoren wegdelen, en er staat juist het omgekeerde van de eerste vergelijking.
groet,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 5 juni 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











