WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bissectricestelling

In een driehoek ABC stellen we BC = a CA = b AB = c .
We trekken de bissectrice van de hoek A en geven het snijpunt met BC de naam D.
Welk veelvoud is vector BD van vector DC?
Jim Va
3de graad ASO - zondag 28 maart 2004

Antwoord

In driehoek ABC met bissectrice AD geldt de zogenoemde bissectricestelling.

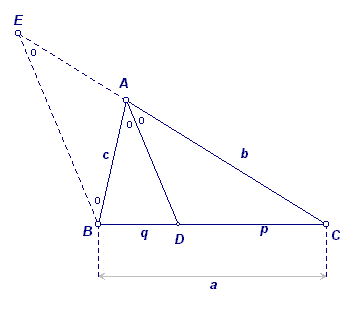
Deze stelling houdt in, dat
AC : AB = CD : BD
of met letters (die de lengte van de lijnstukken aangeven):
b : c = p : q
of ook
b·q = c·p
zodat
q = (c/b)·p of |BD| = (c/b)·|CD|
Het antwoord op de vraag.

De bissectricestelling laat zich eenvoudig bewijzen met behulp van bovenstaande figuur.

De lijn BE is evenwijdig met AD. Dan is direct duidelijk, dat AE = c.
In driehoek CBE (met AD // BE) geldt dan:
CA : AE = CD : BD of b : c = p : q

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 28 maart 2004

Re: Bissectricestelling