|
|
|
\require{AMSmath}



Reeks maken
Hoe vind ik de fourier reeks
van een halve sinus functie.
ik had dit uit een boek: 1/((2^2)-1)cos2t + 1/((4^2)-1)cos2t...
dit is volgens mij niet goed?
Hoe los ik dit juist op en met welke methode?
Peter
Student universiteit BelgiŽ - donderdag 8 januari 2004
Antwoord
Bedoel je de volgende functie?
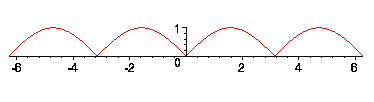
De formule die je uit het boek hebt is dan inderdaad niet correct.
Ten eerste ontbreekt de constante term. Die is gelijk aan de oppervlakte onder een boog, gedeeld door de periode, dus 2/p
Verder weet je dat alle sinustermen coŽfficiŽnt 0 hebben, omdat de functie even is. Je houdt dus alleen cosinustermen over, dus dat klopt wel. Maar de frequenties moeten wel oplopen, dus
c + a1∑cos(2t) + a2∑cos(4t) + ...
Voor het berekenen van an moet je de integraal:
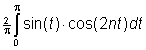
berekenen, en die is niet simpel, maar als je gebruik maakt van de formule
2∑sin(a)∑cos(b) = sin(a+b) + sin(a-b)
dan moet je er wel uitkomen. Let op: het geval n=1 moet je even apart berekenen.
succes,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 9 januari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









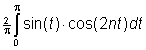


 Re: Reeks maken
Re: Reeks maken