WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Een kermisattractie

Ik moet deze vraag voor school maken en ik kom er helemaal niet uit. Dit is de vraag: Bij een kermisattractie draaien bakjes met zitplaatsen in 2 seconden rond, terwijl de arm waar ze aan vast zitten zelf in 8 seconden ronddraait.
Onderzoek de bewegingen die je maakt als je op 2 m van de as van het bakje zit en de straal van de arm 6 meter is.

Ga ook na hoe je snelheid verloopt gedurende 1 volledige rondgang. Onderzoek in welke richting je beweegt op de tijdstippen waarop de snelheid maximaal of minimaal is.
Evelie
Leerling bovenbouw havo-vwo - zaterdag 2 maart 2002

Antwoord

In het examenprogramma wiskunde B staat: 'De kandidaat kan parametervoorstellingen gebruiken bij het bestuderen van figuren van Lissajous en bij het berekenen van de snelheid waarmee zo'n figuur wordt doorlopen.'

De arm van deze 'attractie' maakt een cirkelbeweging. De parametervoorstelling van zo'n cirkelbeweging met middelpunt O(0,0) en straal r kan je schrijven als:
f(x,y)=(r·cos($\phi$·t),r·sin($\phi$·t))
Hierbij is $\phi$ de hoeksnelheid.

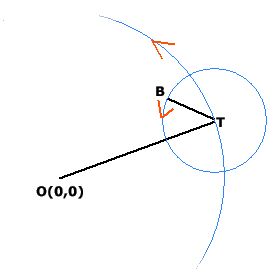
De hoeksnelheid van T is 2$\pi$/8=$\pi$/4 rad/sec en de hoeksnelheid van B is 2$\pi$/2=$\pi$ rad/sec.

Voor T krijg je dan de volgende parametervoorstelling:
T(x,y)=(6·cos($\pi$/4·t,6·sin($\pi$/4·t))

Voor B kan je iets dergelijks doen. Je krijgt dan zoiets als:
B(x,y)=T(x,y)+(...,...)
(dat mag je zelf bedenken!)

Als dat gelukt is kan je met een programma als WinPlot (of met je grafische rekenmachine) de figuur gaan tekenen waarvan je de parametervoorstelling hebt afgeleid.

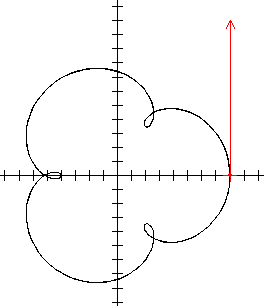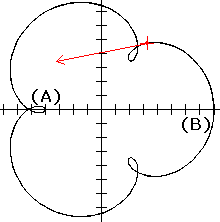
Wanneer is je snelheid het grootst? Als de afgeleide het grootst is!
Hopelijk vind je hier voldoende aanknopingspunten om verder te kunnen.
Zie Grafieken tekenen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 3 maart 2002