WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Injectie, surjectie en bijectie

De vraag is: Onderzoek of de volgende afbeeldingen injectie, surjectie of bijectie zijn. Of geen van beide. Maar ik weet niet hoe ik daar moet aan beginnen.

Vb₁. f : $\mathbf{R}$o+ $\to$ $\mathbf{R}$ : x $\to$ f(x) = ln(x)
Vb₂. f : $\mathbf{R}$ $\to$ $\mathbf{R}$ : x $\to$ f(x) = e^x
Julie
Student Hoger Onderwijs België - maandag 22 december 2003

Antwoord

Het eerste wat je moet doen is een goed 'idee' vormen wat de verschillende begrippen betekenen!

Definities

f is een functie van A$\to$B:
we noemen f een surjectie als er voor alle b$\in$B een a$\in$A bestaat waarvoor geldt b=f(a).
we noemen f een injectie als geldt dat als f(p)=f(q) dan is p=q (anders gezegd: als p$\ne$q dan f(p)$\ne$f(q))
noemen we f een bijectie als de functie injectief en surjectief is (men spreek ook wel van een één-op-één-functie).
Bij je voorbeelden kun je dan deze 'voorwaarden' langs lopen. Hieronder staan ook nog wat tekeningen, kijk er maar eens goed naar!

Vb₁.
Is er voor elke waarde van y een waarde voor x te vinden?
Geldt hier als ln(a)=ln(b) dan a=b?

Vb₂.
Is er voor elke waarde van y een waarde voor x te vinden?
Geldt hier als e^a=e^b dan a=b?

Misschien dat dit plaatje (zie onderstaande website voor betere plaatjes) kan helpen:

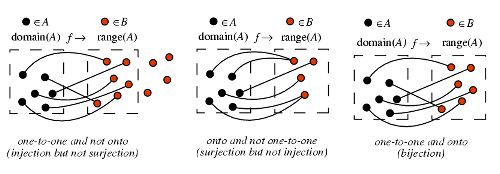
...en anders maar weer vragen.

Zie ook Surjectief/injectief en Verschil injectief en bijectief
Zie Mathworld Wolfram - Injection

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 22 december 2003