|
|
|
\require{AMSmath}



Een punt op een cirkel berekenen adhv een rotatie
Gegeven:
# Middelpunt cirkel (mx,my)
# Een punt a op de cirkel gekend door de afstanden x en y tot dat punt vanuit het middelpunt (Als het middelpunt dus op (0,0) zou liggen zou a op (x,y) liggen)
# Een rotatie in graden waarbij a als 0į wordt aanzien
Vraag:
# De coordinaten van punt b dat op [rotatie]į van punt a ligt.
Dank bij voorbaat,
E Geys
Student Hoger Onderwijs BelgiŽ - zaterdag 6 december 2003
Antwoord
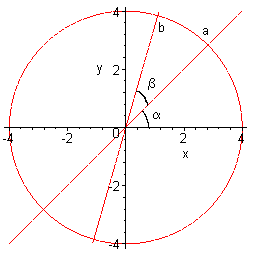
stel a(xa,ya) dan is
(xa,ya)=(R cos(a), R sin(a) )
en stel b(xb,yb) dan is
(xb,yb)=(R cos(a+b), R sin(a+b) )
=(R cos(a)cos(b)-R sin(a)sin(b), R sin(a)cos(b)+sin(b)cos(a))
Hier de coŲrdinaten van a in invullen en dan nog een kleine transformatie naar een willekeurig middelpunt. Lukt het nu?
Mvg,
Els
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








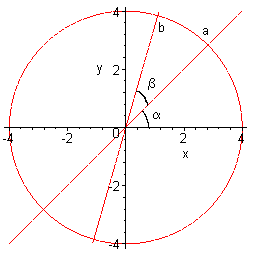

 Re: Een punt op een cirkel berekenen adhv een rotatie
Re: Een punt op een cirkel berekenen adhv een rotatie