|
|
|
\require{AMSmath}



Leerlingen per 2 op schoolbanken
Hallo,
Op hoeveel manieren kan je 10 leerlingen per 2 op 5 schoolbanken schikken, maar zo waarbij de links-rechtsvolgorde niet mag meegeteld worden? Met 4 personen heb je 24 mogelijkheden maar met mijn beperking slechts 6: AB CD,CD AB,AC BD,BD AC,AD BC en BC AD.
Als ik correct heb gerekend, kom ik voor 8 personen uit op 2520 mogelijkheden. Wat is de formule daarvoor?
Bestaat er een computerprogramma om de volledige lijst mogelijkheden te genereren?
vanden
Iets anders - vrijdag 5 december 2003
Antwoord
Je kunt dit als volgt aanpakken.
Je weet waarschijnlijk dat het aantal mogelijkheden om k personen te kiezen uit een verzameling van n personen, gelijk is aan (n boven k).
Jouw probleem kun je als volgt aanpakken (voor 10 personen)
Voor de eerste bank kies je 2 personen uit 10.
Dat kan op (10 boven 2) manieren.
Bij elk van die manieren heb je nog 8 personen over.
Voor de tweede bank kies je dus 2 personen uit 8.
Dat kan op (8 boven 2) manieren.
Voor de derde bank heb je nog (6 boven 2) manieren
Voor de tweede bank nog (4 boven 2)
En de laatste bank is dan geen keuze meer. (2 boven 2) is gelijk aan 1.
Het aantal mogelijkheden is dus:
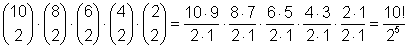
In het algemeen voor 2p personen: (2p)! gedeeld door 2p
Het berekenen van het aantal mogelijkheden is dus geen probleem meer, maar het genereren van een volledige lijst mogelijkheden is wat anders.
Hieronder zie je een link naar een andere vraag, waar een programma bij gemaakt is. Misschien heb je daar wat aan.
groet,
Zie programma dat combinaties genereert

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 8 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|