|
|
|
\require{AMSmath}



Parabool
Gegeven: richtlijn x-y=1
brandpunt (2;-1)
Gevraagd: vergelijking van de parabool
Hoe ga je hier te werk op de kortste manier?
Bepaal je eerst de evenwijdige aan de richtlijn door het brandpunt? En als je dat dan doet, wat ben je daarmee verder?
Of bepaal je de loodrechte op de richtlijn door het brandpunt? En wat ben je daar dan mee?
Alvast heel erg bedankt voor de vorige antwoorden!
Bea Ve
Student Hoger Onderwijs BelgiŽ - donderdag 14 augustus 2003
Antwoord
De parabool is de meetkundige plaats van de punten die op gelijk afstand liggen van de richtlijn en het brandpunt.
De lopende coordinaat geven we de naam (x,y) zoals gewoonlijk.
Eerst bepalen we de parametervoorstelling van de richtlijn:
(t,t-1)
De afstand van de lopende coordinaat tot het brandpunt is gemakkelijk: ÷((x-2)2+(y+1)2)
De afstand van de lopende coordinaat tot de richtlijn is dus de kortste afstand tussen de lopende coordinaat en een punt op die richtlijn. Die afstand is dus ÷((x-t)2+(y+1-t)2) ge minimaliseerd.
(minimaliseren doe je door af te leiden naar t en die nul te stellen, en daar t uit op te lossen)
Je krijgt dan voor de waarde van t= 1/2 x + 1/2 y + 1/2
Dus de kortste afstand tussen de lopende coordinaat en de richtlijn is (door de waarde van t in de afstand in te vullen)
÷((x-1/2 x + 1/2 y + 1/2)2+(y+1-1/2 x + 1/2 y + 1/2)2)
na uitwerking:
(1/2*x-1/2*y-1/2)2+(1/2*y-1/2*x+1/2)2
De twee vetgedrukte uitdrukkingen stel je aan elkaar gelijk (want het zijn die afstanden die gelijk moeten zijn wil een punt (x,y) op de parabool liggen). Dit geeft de vergelijking van de parabool: -1/2*x≤-1/2*y≤-x*y+3*x-y-9/2 = 0
Alles ziet er zo uit:
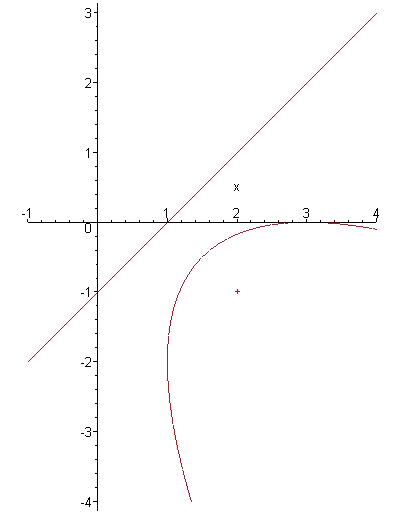
Koen Mahieu

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 augustus 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








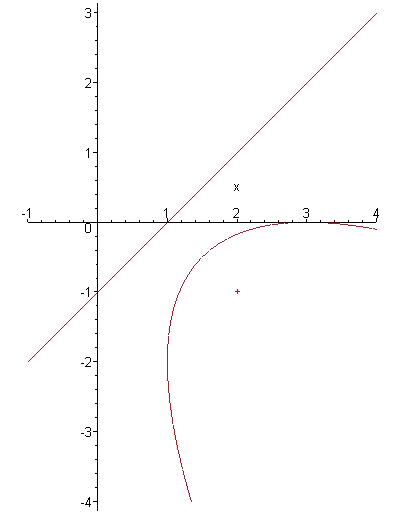


 Re: Parabool
Re: Parabool