1. Ontbinden in factoren

Bij het oplossen van tweedegraads (of hogere graads) vergelijkingen gebruik je vaak een belangrijke eigenschap van vermenigvuldigen.

Als a · b = 0, dan geldt:
a = 0 of b = 0

Dat betekent dat als een product (het resultaat van een vermenigvuldiging) de waarde nul heeft, minstens één van de factoren (de 'dingen' die je met elkaar vermenigvuldigt) nul moet zijn.
Dit kun je gebruiken om vergelijkingen op te lossen.

Voorbeeld
x · (x + 1) = 0

Je hebt hier te maken met twee factoren: x en x + 1.
Eén van deze twee factoren moet nul zijn, dus:
x = 0 of x + 1 = 0
Conclusie: x = 0 of x = -1.

Niet alle vergelijkingen bestaan natuurlijk uit een product, maar vaak kun je er voor zorgen dat er wel een product komt te staan.

Voorbeeld
x² + x = 0
kun je schrijven als:
x · (x + 1) = 0
Deze bewerking heet ontbinden (in factoren).
Je hebt de vergelijking x² + x = 0 herschreven als een product dat de waarde nul heeft. Dit laatste type vergelijkingen kun je oplossen met de 'eigenschap' van producten (zie boven).

Voordat je gaat ontbinden moet je de vergelijking op nul herleiden.

Voorbeeld
x³ = 2x²
x³ - 2x² = 0
x² · (x - 2) = 0
x² = 0 of x - 2 = 0
x = 0 of x = 2

Samengevat:

Eerst op nul herleiden
Ontbinden in factoren
Gebruik "Als a · b = 0, dan a = 0 of b = 0"

Ontbinden in factoren

Bij tweedegraads verdelijkingen kan je twee soorten van ontbinden in factoren toepassen:

Een zo groot mogelijke term buiten haakjes halen.
Van een drieterm een product van 2 tweetermen maken.

Deze laatste soort staat wel bekend onder de naam product-som methode.

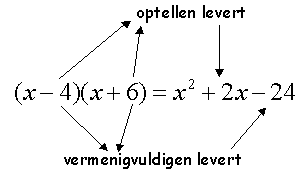
Voorbeeld
x² + 8x + 12 kun je ontbinden als (x + 6)(x + 2).
Controle:
(x + 6)(x + 2) = x² + 2x + 6x + 12 = x² + 8x + 12
Klopt!

De vraag is nu: hoe kun je zo'n ontbinding vinden?

Laten we eens kijken naar wat voorbeelden:
(x + 2)(x + 3) = x² + 5x + 6
(x + 2)(x-3) = x² - x - 6
(x + 1)(x - 4) = x² - 3x - 4
(x - 4)(x - 4) = x² - 8x + 16
(x - 3)(x + 3) = x² - 9

Als het goed is vallen er twee dingen op:

Het getal voor de x aan de rechter kant is de som (optellen dus) van de twee getallen aan de linker kant.
Het getal aan de rechter kant is het product (vermenigvuldigen dus) van de twee getallen aan de linker kant.

Schematisch:

Nu andersom:

Je wilt een ontbinding vinden voor x² + 7x + 12
Op grond van het bovenstaande moet je twee getallen zoeken die opgeteld 7 zijn en vermenigvuldigd 12.
Mogelijke kandidaten (alle mogelijke tweetallen met als product 12):

Product

1 · 12

2 · 6

3 · 4

-1 · -12

-2 · -6

-3 · -4

Als je nu ook nog naar de som kijkt, krijg je volgende tabel:

Product	Som
1 · 12	13
2 · 6	8
3 · 4	7
-1 · -12	-13
-2 · -6	-8
-3 · -4	-7

Ik zocht twee getallen met product 12 en som 7, dus 3 en 4.
Je kunt x² + 7x + 12 dus ontbinden als (x + 3)(x + 4)

Vaak is het niet nodig (of zelfs verstandig) om zo'n tabel te maken. Als je goed kijkt (en nadenkt) kun je het soms zo zien.

Voorbeeld
x² - 4x = 21
x² - 4x - 21 = 0
(x - 7)(x + 3)=0
x - 7 = 0 of x + 3 = 0
x = 7 of x = -3

Voorbeeld
2x⁴ - 8x³ = 42x²
x⁴ - 4x³ = 21x²
x⁴ - 4x³ - 21x² = 0
x² · (x² - 4x - 21) = 0
x² = 0 of x² - 4x - 21 = 0
x = 0 of (x - 7)(x + 3)=0
x = 0 of x - 7 = 0 of x + 3 = 0
x = 0 of x = 7 of x = -3

Voorbeeld
x³ = x² + 12x
x³ - x² - 12x = 0
x(x² - x - 12) = 0
x = 0 of x² - x - 12 = 0
x = 0 of (x - 4)(x + 3) = 0
x = 0 of x = 4 of x = - 3

Voorbeeld
x⁴ - 8·x² - 9 = 0
neem y=x²
y² - 8y - 9 = 0
(y - 9)(y + 1)
y = 9 of y = - 1
x² = 9 of x² = - 1
x² = 9
x = - 3 of x = 3

Voorbeeld
x⁶ - 16x³ + 64 = 0
neem y=x³
y² - 16y + 64 = 0
(y - 8)(y - 8) = 0 of (y - 8)² = 0
y = 8
x³ = 8
x = 2

Voorbeeld
x - 13√x + 36 = 0
neem y=√x
y² - 13y + 36 = 0
(y - 9)(y - 4) = 0
y = 9 of y = 4
√x = 9 of √x = 4
x = 81 of x = 16

Voorbeeld
(x - 4)² - 5(x - 4) + 6 = 0
neem y=x-4
y² - 5y + 6 = 0
(y - 3)(y - 2) = 0
y = 3 of y = 2
x - 4 = 3 of x - 4 = 2
x = 7 of x = 6

Voorbeeld
2x² - (x - 2)² = 1
2x² - {x² - 4x + 4} = 1
2x² - x² + 4x - 4 = 1
x² + 4x - 5 = 0
(x + 5)(x - 1) = 0
x = - 5 of x = 1