WisFaq!

Re: Oppervlakte bol

Alvast bedankt met de bol ga ik even proberen maar op de beschreven website kan ik alleen maar vinden hoe je de inhoud van een torus kunt berekenen en niet de oppervlakte, dus kan je me daar nog mee verder helpen?

chantal
15-4-2003

Antwoord

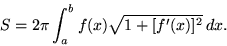
is de algemene formule voor de manteloppervlakte van het omwentelingslichaam dat je bekomt door de kromme f(x) te wentelen rond de x-as.

In het geval van een torus moet je dat in twee stappen doen:

(r straal van de 'buis', R afstand van het midden van de buis tot het midden van de torus)

1) f(x) = R + √(r²-x²), dit is de buitenste helft van de torus, die je bekomt door de bolle helft van de cirkel te wentelen rond de x-as. Je bekomt S1 = 4$\pi$r²+2$\pi$²rR

2) f(x) = R - √(r²-x²), dit is de binnenste helft van de torus, die je bekomt door de holle helft van de cirkel te wentelen rond de x-as. Je bekomt S2 = -4$\pi$r²+2$\pi$²rR

Totale oppervlakte S = S₁ + S₂ = 4$\pi$²Rr

cl
16-4-2003