WisFaq!

Re: Een gezin van vier

Bedankt! Het antwoord schijnt 53,99% te zijn, maar ik weet niet hoe ik dit zou moeten berekenen, ook niet met deze extra uitleg. Je weet dat het of 4 jongens zijn of 4 meisjes. Heel eerlijk gezegd zou ik denken dat de kans 51% is omdat de kans op jongens 51% is en op meisjes 49%.

Esmee
25-6-2024

Antwoord

Hallo Esmee,

De kans op een jongen is 0,51. De kans op twee jongens is 0,51 $\times $ 0,51=0,2601, enz. De kans op 4 jongens is 0,51⁴ $\approx$ 0,06765.
Op dezelfde manier vind je: de kans op 4 meisjes is 0,49⁴ $\approx$ 0,05765.

Stel dat je 10000 gezinnen beschouwt met 4 kinderen. Dan verwacht je:

• Aantal gezinnen met 4 jongens: 0,06765 $\times $ 10000=6765 gezinnen
  
• Aantal gezinnen met 4 meisjes: 0,05765 $\times $ 10000=5765 gezinnen
  
  
• Totaal aantal gezinnen met 4 kinderen: 6765+5765=12530

Als je dan alleen de gezinnen beschouwt met 4 kinderen van hetzelfde geslacht (dus: 12530 gezinnen), dan is de kans dat het alleen jongens zijn, gelijk aan⁶⁷⁶⁵/₁₂₅₃₀ $\approx$ 0,5399, ofwel 53,99%.

Ik kan goed begrijpen dat dit tegen je gevoel in gaat, ik kan me voorstellen dat je 51% zou verwachten. Toch is het wel te begrijpen dat dit niet klopt, het wordt gemakkelijker om dit te zien wanneer er een groter verschil is tussen de kans op een jongen of een meisje.

Stel dat de kans op een jongen 90% is, en de kans op een meisje 10%. Ga uit van 100 gezinnen. Als er 1 kind wordt geboren, dan verwacht je 0,9 $\times $ 100=90 'jongensgezinnen' (= gezinnen met alleen jongens als kind) en 0,1 $\times $ 100=10 meisjesgezinnen. Dit zie je in het linkerdeel van onderstaand boomdiagram.



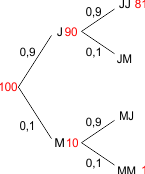
Nu wordt een tweede kind geboren. In de jongensgezinnen (waarvan er al veel zijn) lukt het in 90% van de gevallen om een kind van hetzelfde geslacht te krijgen. Van het grote aantal jongensgezinnen blijft dus een groot deel jongensgezin, nu met twee kinderen (jongens). Na twee kinderen komt het aantal jongensgezinnen op 0,9 $\times $ 0,9 $\times $ 100=81 (zie het rechter deel van het boomdiagram).
Bij de meisjesgezinnen (waarvan er al veel minder waren) lukt het maar in een klein aantal gevallen (10%) om opnieuw een kind van hetzelfde geslacht te krijgen. Van het kleinere aantal meisjesgezinnen blijft naar verhouding een veel kleiner deel over: slechts 10%. Het aantal meisjesgezinnen komt op 0,1 $\times $ 0,1 $\times $ 100=1.
Na twee kinderen zijn in totaal nog 81+1=82 gezinnen met kinderen van hetzelfde geslacht, hiervan zijn 81 jongensgezinnen. De kans dat een gezin met twee kinderen van hetzelfde gelacht een jongensgezin is, komt hiermee op ⁸¹/₈₂ $\approx$ 0,988, ofwel 98,8%.
Na elk kind neemt het aantal meisjesgezinnen sterker af dan het aantal jongensgezinnen. De kans dat een gezin met kinderen van hetzelfde gelacht een jongensgezin is, wordt na elk kind dus steeds groter. Bij een kleiner verschil in kans, zoals bij jouw vraag, is dit effect minder groot, maar wel aanwezig.

Is het hiermee duidelijker geworden?

GHvD
25-6-2024