WisFaq!

Re: Driehoek met omschreven cirkel

Veel dank voor het antwoord, het gaat mij alleen even iets te snel. Hoe weten we zo zeker dat de hoek BAD 90 graden en hoek ABD 30 graden is (ondanks dat het suggestief is door het plaatje)? Hoe komt u ook aan de verhouden 1:2: $\sqrt{3} $

Erik-Jan
26-5-2024

Antwoord

Hallo Erik-Jan,

Goed dat je doorvraagt wanneer (een deel van) een antwoord niet duidelijk is. Wij weten immers niet hoeveel achterliggende kennis je al hebt.



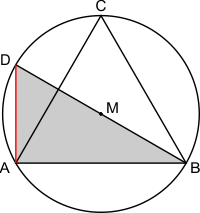
Allereerst hoek BAD. Je had zelf al gevonden dat BD een middellijn is van de cirkel. Voor elk punt A op de cirkel geldt dan dat hoek BAD een rechte hoek is, zie wikipedia: Stelling van Thales.

Dan hoek ABD. Trek vanuit M de hulplijnen MA, MB en MC, zie hieronder:



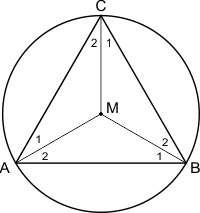
Zo ontstaan drie gelijke driehoeken AMB, BMC en CMA. Deze driehoeken zijn gelijkbenig, want de zijden MA, MB en MC zijn alle gelijk aan de straal van de cirkel. Hierdoor zijn de hoeken A₁, A₂, B₁, B₂, C₁ en C₂ allemaal gelijk. Elk van deze hoeken is zodoende ^180°/₆=30°. Dan blijft over voor hoek ADB: 180°-90°-30°=60°.

Driehoek BDA is een zgn. "30-60-90-graden driehoek", deze heeft vaste verhoudingen tussen de zijden. Dit kan je in de figuur hieronder zien. Driehoek PQR is zo'n 30-60-90-graden driehoek, deze is nog eens gespiegeld om PQ:



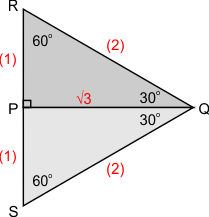
Op deze wijze ontstaat de gelijkzijdige driehoek SQR, met drie gelijke hoeken van 60°. De zijden van deze driehoek zijn 2, dus QR=2. P is het midden van RS, dus PR=1. Met Pythagoras is PQ dan te berekenen:

PQ = √(2²-1²) = √(4-1) = √3.

De driehoek met hoeken 30°, 60° en 90° komt veel voor, dus veel mensen nemen niet meer de moeite om bovenstaande afleiding steeds opnieuw te maken, maar leren uit het hoofd dat de zijden van zo'n "30-60-90-graden driehoek" zich verhouden als 1:2:√3. Hou hierbij goed in de gaten welke lengte bij welke zijde hoort: korte rechthoekszijde:schuine zijde:lange rechthoekszijde.

In onderstaande figuur geldt dus:



AD:AB = 1:√3
dus:
AD = ^AB/_√3 = ¹/_√3 = ¹/₃√3.

OK zo?

GHvD
26-5-2024