P(A)+P(B) = P(A\mathbin{\text{or}} B)+P(A\mathbin{\text{and}} B)
Kijk naar het onderstaande plaatje, waar ik `or' vervangen heb door \cup (vereniging) en `and' door \cap (doorsnede).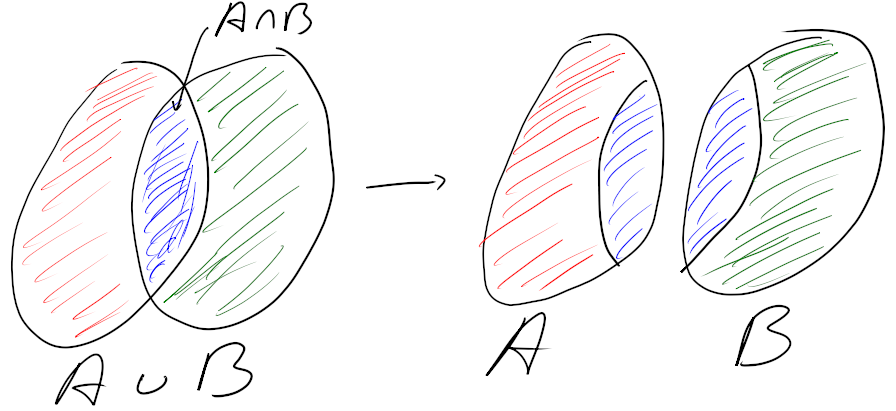
Rechts zie je A en B losgemaakt van elkaar, het blauwe stuk is de doorsnede (het `en'-gedeelte) en dat wordt twee keer geteld als je P(A)+P(B) bepaalt.
In P(A\cup B) worden de drie stukken elk één keer geteld dus moet je bij P(A\cup B) nog P(A\cap B) optellen om P(A)+P(B) te krijgen.
Over kansrekening en wat daarmee samenhangt zijn veel boeken te vinden, bijvoorbeeld Kansrekening van Alex van den Brandhof (als je op die site naar `Kansrekening zoekt vindt je nog meer boeken).
kphart
2-4-2024