Ik heb Maple te hulp geroepen en die geeft, voor de uitdrukking in $\Omega$:
$$
R(x,y)=1+x^{4}-6 x^{2} y^{2}+y^{4}-\left(4 \zeta^{2}+2 k +2\right) \left(x^{2}-y^{2}\right)+k +4 \zeta \left(3 x^{2} y -y^{3}\right)-4 \zeta k y -4 \zeta y
$$
en
$$
I(x,y)=4 x^{3} y -4 x \,y^{3}-2 \left(4 \zeta^{2}+2 k +2\right) x y -4 \zeta \left(x^{3}-3 x \,y^{2}\right)+4 \zeta k x +4 \zeta x
$$
(ik heb de indices aan $\zeta$ en $k$ even weggelaten).
De functie die je wilt plotten wordt dan
$$
k*\bigl(R(x,y)^2+I(x,y)^2\bigr)^{-\frac12}
$$
Daar zou wolfram alpha geen problemen mee moeten hebben.
Ik heb ontdekt dat Maple precies doet wat je wilt, definieer
$$
f(z)=z^{4}-4 \,j \zeta \,z^{3}-2 \left(2 \zeta^{2}+k +1\right) z^{2}+4 \,j \zeta \left(1+k \right) z +1+k
$$
($z$ in plaats van $\Omega$).
Het commando
complexplot3d(g(z), z=a+b*I..c+d*I);
geeft een plot van de modulus van de gegeven functie $g(z)$ over de rechthoek tussen $a+bj$ en $c+dj$.
Dus wat jij moet hebben krijg je met
complexplot3d(k/f(z), z=a+b*I..c+d*I);
Hier is een voorbeeld met $\zeta=k=1$ en $z=(0.1+0.1j)\, ..\, (1+j)$
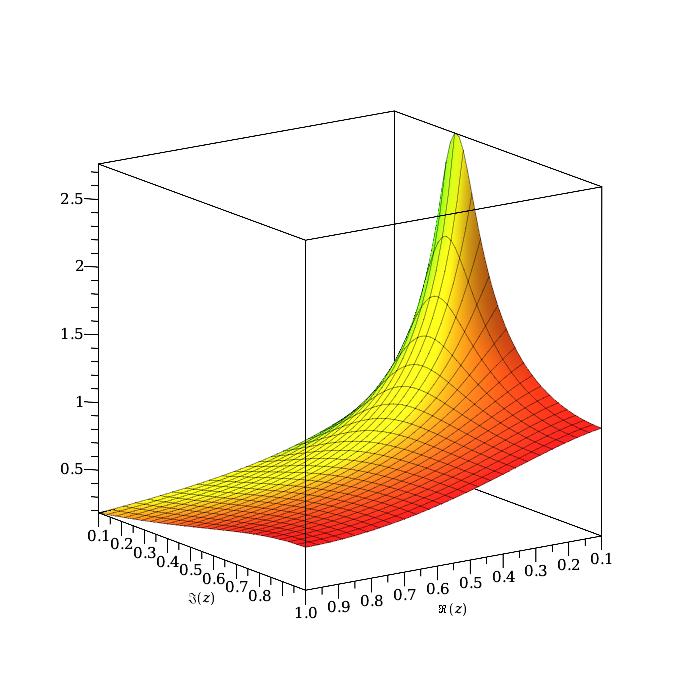
kphart
15-2-2024