WisFaq!

Oppervlakte onder grafiek met gespiegelde functie

Beste,

In de bijlage de opgave, mijn uitwerking en het antwoordmodel. De werkwijze snap ik maar ik snap niet hoe ze aan de factor 2e - de integraal komen.

Groet,

Jan

---

• Opgave
• Antwoord
• Uitwerking

---

Jan
28-5-2023

Antwoord

Hallo Jan,

Je vergat te vermelden om welke functie het gaat, maar uit de uitwerkingen begrijp ik dat het gaat om f_e(x)=ln(ex).

Wanneer je x als functie van y schrijft (dus x en y verwisselt), dan krijg je inderdaad:

y = ¹/_e·e^x

De grafiek (met horizontaal de 'nieuwe' x en verticaal de 'nieuwe' y) ziet er dan zo uit:



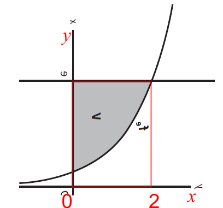
Het vlakdeel V waarvan je de oppervlakte moet bepalen, is nu een oppervlakte boven de curve in plaats van onder onder de curve. Je berekent de gevraagde oppervlakte door de oppervlakte van de rode rechthoek te berekenen (deze is 2e) en daarvan de witte oppervlakte onder de curve af te trekken (de door jou berekende witte oppervlakte onder de curve).

GHvD
29-5-2023