WisFaq!

Stand-by tijd van mobiel

Opgave 6: (6 punten)

Volgens een fabrikant is de stand-by tijd van zijn mobiele telefoons minstens 120 uur. De consumentenbond verwerpt de bewering van de fabrikant, want bij een steekproef van lengte n is de gemiddelde stand-by tijd 117,6 uur. Hierbij is een significantieniveau van 2.5% genomen en is uitgegaan van een standaardafwijking van een standaardafwijking van 5 uur.`

• Van hoeveel mobiele telefoons heeft de consumentenbond minstens de stand-by tijd gemeten?

jasmina
31-3-2023

Antwoord

Hallo Jasmina,

De kansvariabele X is de gemiddelde stand-by tijd van deze telefoons.

De nulhypothese is: X=120
Alternatieve hypothese: X $<$ 120

Dit wordt een éénzijdige toets, omdat de kwaliteit van de telefoon alleen bij een te korte stand-by tijd onvoldoende is, niet bij een te lange stand-by tijd.

Maak voor het inzicht een schets, deze gaat ervan uit dat de nulhypothese waar is. Dan is de gemiddelde stand-by tijd 120 uur, de gemiddelde stand-by tijd binnen een steekproef van n telefoons heeft dan een standaardafwijking van ⁵/_√n. Je schets ziet er dan zo uit:



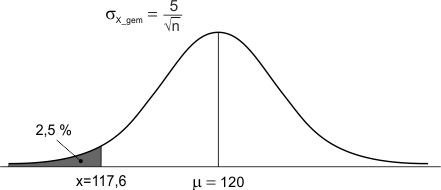
De nul-hypothese wordt verworpen wanneer het steekproefresultaat bij de aanname 'gemiddelde=120' te onwaarschijnlijk is. In dit geval: wanneer de kans op dit resultaat minder is dan 2,5%. Ofwel: De kans op een steekproefresultaat "gemeten tijd = 117,6 uur" is maximaal 0,025.
Bereken dus welke standaardafwijking $\sigma$_{X_gem} hoort bij de schets hierboven. Ik kom op ongeveer 1,22.
Los dan de vergelijking ⁵/_√n=1,22... op om de gevraagde minimale steekproefomvang n te vinden.

Let op: voor n vind je vast geen geheel getal. Omdat dit een minimale waarde is om aan de vraag te voldoen, moet je altijd naar boven afronden om de minimale steekproefomvang te vinden.

GHvD
1-4-2023