WisFaq!

Re: Overlapping bij diagonaal vouwen van een rechthoekig vel

Zeer bedankt, Gilbert!
Maar nu wanneer je een hoek naar de diagonaal tegenoverliggende hoek vouwt. Je houdt dan een vijfhoek over. Wat is dan het 'verlies' aan oppervlakte tov van de oorspronkelijke rechthoek? Kom ik dan in de goniometrie?

... en bij voorbaat dank!

Jan Karman
12-1-2023

Antwoord

Hallo Jan,

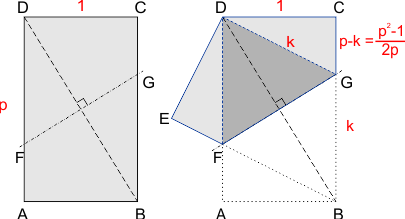
Laten we uitgaan van een rechthoekig vel met breedte=1 en lengte=p, zie de figuur links hieronder. Het vel wordt over lijn FG gevouwen, de vouwlijn FG is de middelloodlijn van de diagonaal BD. Hierdoor komt hoekpunt B op hoekpunt D te liggen, zie de figuur rechts.



Voor de oppervlakte van het papier geldt:

• Opp. papier = 1xp = p (1)

Na het vouwen heeft het geheel een vijfhoekige vorm CDEFG, waarbij driehoek DFG bestaat uit twee lagen.

De rand BG wordt na vouwen het lijnstuk DG, dus BG=DG. Ik noem de lengte van deze lijnstukken k. Voor CG blijft dan een lengte p-k over.
Volgens Pythagoras geldt in driehoek DCG:


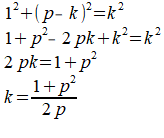
Voor CG=p-k geldt dan:


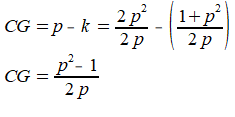
De driehoeken DCG en DEF (enkele laag papier) vormen samen een rechthoek met lengte=1 en breedte=^(p2-1)/_2p, de oppervlakte van deze 'uitstekende' driehoeken samen is dus:

• Opp. enkele laag = ^(p2-1)/_2p (2)

Dan blijft over aan materiaal voor de twee overlappende driehoeken (1)-(2):



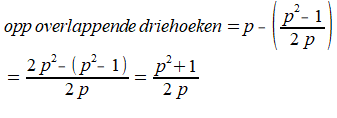
Driehoek DFG heeft als oppervlakte de helft hiervan:



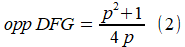
Hiermee berekenen we de oppervlakte van vijfhoek CDEFG:



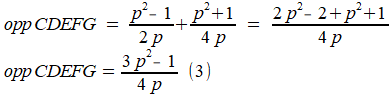
Het percentage overlap in vijfhoek CDEFG is (2)/(3) x 100%:



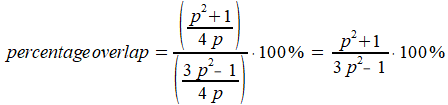
De oppervlakte van vijfhoek CDEFG als percentage van de oppervlakte van het oorsprobkelijke vel is (3)/(1) x 100%:



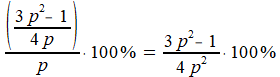
OK zo?

GHvD
13-1-2023