WisFaq!

Ontbinden in factoren

Ik kom er niet uit bij het ontbinden van factoren en dan het buiten halen van van de haakjes. met een voorbeeld k²+k-42 dat lukt mijn niet ik zou het graag willen dat u mij zou helpen nog een voorbeeld k³-4k en k³+5k²+4k

elly dabrowski
6-4-2003

Antwoord

'Normaal' gesproken zijn er twee soorten van ontbinden in factoren:

• Een zo groot mogelijke term buiten haakjes halen.
  
• Van een drieterm een produkt van 2 tweetermen maken.

Deze laatste soort staat wel bekend onder de naam produkt-som methode of som-produkt methode.

Voorbeeld
x² + 8x + 12 kun je ontbinden als (x + 6)(x + 2).
Controle:
(x + 6)(x + 2) = x² + 2x + 6x + 12 = x² + 8x + 12
Klopt!

De vraag is nu: hoe kun je zo'n ontbinding vinden?
Laten we eens kijken naar wat voorbeelden:

(x + 2)(x + 3) = x² + 5x + 6
(x + 2)(x-3) = x² - x - 6
(x + 1)(x - 4) = x² - 3x - 4
(x - 4)(x - 4) = x² - 8x + 16
(x - 3)(x + 3) = x² - 9

Als het goed is vallen er twee dingen op:

• Het getal voor de x aan de rechter kant is de som (optellen dus) van de twee getallen aan de linker kant.
  
• Het getal aan de rechter kant is het produkt (vermenigvuldigen dus) van de twee getallen aan de linker kant.

Schematisch:



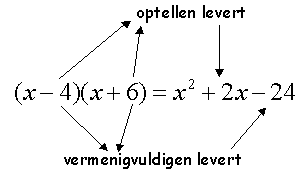
Nu andersom:

Je wilt een ontbinding vinden voor x² + 7x + 12
Op grond van het bovenstaande moet je twee getallen zoeken die opgeteld 7 zijn en vermenigvuldigd 12.
Mogelijke kandidaten (alle mogelijke tweetallen met als produkt 12):

Produkt

1 · 12

2 · 6

3 · 4

-1 · -12

-2 · -6

-3 · -4

Als je nu ook nog naar de som kijkt, krijg je volgende tabel:

Produkt	Som
1 · 12	13
2 · 6	8
3 · 4	7
-1 · -12	-13
-2 · -6	-8
-3 · -4	-7

Ik zocht twee getallen met produkt 12 en som 7, dus 3 en 4.
Je kunt x² + 7x + 12 dus ontbinden als (x + 3)(x + 4)

Vaak is het niet nodig (of zelfs verstandig) om zo'n tabel te maken. Als je goed kijkt (en nadenkt)
kun je het soms zo zien.

k²+k-42:
Met de produkt-som-methode! We zoeken twee getallen die opgeteld 1 zijn en vermenigvuldigd -42. Mogelijk kandidaten zijn:
1·-42 de som is -41
2·-21 de som is -19
3·-14 de som is -11
6·-7 de som is -1
...maar ook:
-1·42 de som is 41
-2·21 de som is 19
-3·14 de som is 11
-6·7 de som is 1
Ah.. de laatste is het!
Dus k²+k-42=(k-6)(k+7)

k³-4k
Dit is een typisch geval van k buiten haakjes halen! Dus schrijven we:
k³-4k=k(k²-4)

Nu bestaat er ook nog zoiets als het merkwaardig produkt!? (zie zoeken). Eén van die merkwaardige produkten zegt:
a²-b²=(a+b)(a-b)
Toegepast op k(k²-4) krijg je dan nog:
k³-4k=k(k²-4)=k(k+2)(k-2)

Je kunt hierbij ook denken aan de produkt-som-methode! Ik zoek twee getallen die opgeteld nul en vermenigvuldigd -4 zijn. Dat zijn -2 en 2.
k³+5k²+4k
Ook hier kan je een 'k' buiten haakjes halen. Dus schrijven we:
k³+5k²+4k=k(k²+5k+4)

Voor het deel tussen de haakjes kan je de produkt-som-methode gebruiken:
k²+5k+4
Ik zoek weer twee getallen die opgeteld 5 en vermenigvuldigd 4 zijn. Dat zijn 1 en 4.
Dus:
k³+5k²+4k=k(k²+5k+4)=k(k+4)(k+1)

Hopelijk kan je zelf verder. Kijk ook even op onderstaande website voor meer voorbeelden!

Zie Ontbinden in factoren [http://users.kbc.skynet.be/ontbfac/]

WvR
6-4-2003