WisFaq!

TI-83 MODE/Seq

Kunnen jullie mij uitleggen hoe je het deel van je GR gebruikt, als je hem bij MODE op Seq zet?
Dan kun je dingen doen bij Y= enzo en ik zag ook ergens staan dat je dan ook in het basisscherm dingen kan intikken als v(40)-v(90) en dat je dan een antw krijgt

Misschien kunnen jullie het kort uitleggen aan de hand van het volgende sommetje:

40
$\sum$(3^k+k²+2)
k=10

Anne
6-4-2003

Antwoord

Zet de rekenmachine bij MODE op Seq.
Voer het scherm bij Y= als volgt in:




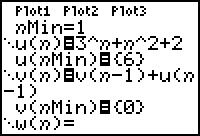
Bij u(n) staat de rij waarover je de som wilt nemen.
nMin=1 betekent dat je de rij laat beginnen bij n=1.
u(nMin) = u(1) = 6.

Bij v(n) komt de somrij te staan. Je neemt de vorige waarde van de somrij (v(n-1)) en telt daar de nieuwe waarde van de rij u bij op.
De u krijg je met 2nd 7 en de v met 2nd 8.
v(nMin) = 0, omdat je aan het begin nog geen som hebt.

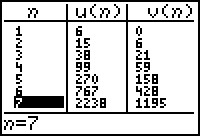
Kijken we nu in de tabel, dan zie je daar bij u(n) de gewonen rij en bij v(n) de somrij. Let alleen op dat de elementen uit de somrij net een verschoven zijn.




Willen we nu jouw sommatie uitrekenen, dan kan je dit doen door in te voeren: v(41)-v(11)




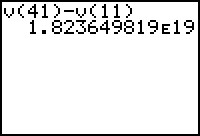
Deze sommatie uitrekenen kan echter veel sneller.
Zet je rekenmachine in MODE weer op Func. (Dit is niet noodzakelijk, maar je rekenmachine zal waarschijnlijk meestal in deze stand staan.)
Voer in de rekenmachine het volgende commano in:
sum(seq(3^X+X²+2,X,10,40))
De optie sum( vind je onder LIST (2nd STAT), menu MATH, optie 5. De optie seq( vind je onder LIST, menu OPS, optie 5.



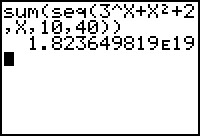
Het commando seq( maakt een rij. Achter seq( zet je eerst de formule van de rij, dan de variabele in de rij, gevolgd door het laagste en het hoogste rangnummer.
Het commando sum( telt de elementen uit een rij op.

Wanneer je de rij in de directe rangnummer vorm hebt, heeft de optie seq( de voorkeur.
Wanneer je de rij in de indirecte recursieve vorm hebt, kun je beter MODE Seq gebruiken.

wh
9-4-2003