Allereerst zullen we moeten afspreken WAT je onder tekenen verstaat. In de meetkunde is het (al vanaf de oude Grieken)gebruikelijk om figuren te construeren (tekenen) met ALEEN het gebruik van een passer en een liniaal (zonder verdeling, dus een latje). Je kan dus slechts lijnen (of lijnstukken) door twee punten tekenen en een cirkel met een gegeven middelpunt die door een ander gegeven punt gaat.
Daarnaast moet je de gegevens juist interpreteren cq. juist formuleren.
Zoals jij het stelt gaat het denk ik NIET. Kijk maar in de onderstaande figuur, links.
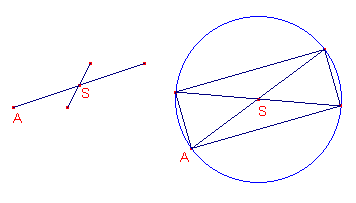
Je vertelt er namelijk niet bij, dat de beide diagonalen (lijnstukken) even lang moeten zijn.
Gaan we uit van twee gelijke lijnstukken die elkaar in het punt S middendoor delen, dan is de rechthoek snel geconstrueerd. Via een cirkel met S als middelpunt en een van de eindpunten van een lijnstuk als tweede punt (bijvoorbeeld het punt A).
Maar dan komt het eigenlijk pas.
Je moet nu bewijzen, dat er inderdaad een rechthoek geconstrueerd is.
Allereerst moet je bewijzen, dat die cirkel ook door de andere drie punten gaat (da's niet zo erg moeilijk).
Maar dat het een rechthoek is!
Dat vereist toch nog wel enig nadenken!
Overigens, ook het construeren (ja dat moet ook) van de beginsituatie is soms nog wel eens een probleem.
Hoe doe je dat in het geval van jouw rechthoek?
En dan nu het antwoord op je vraag.
Het kost soms heel wat moeite om het te "zien" (niet in de zin van kijken dus).
En een algemene methode is helaas niet te geven.
Zie Rekenen in het Oude Egypte [http://info.math4all.nl/Wiskundegeschiedenis/Onderdelen/RGEgypte.html]
WvR
3-4-2003