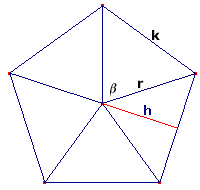
De hoekpunten van zo'n n-hoek liggen op een cirkel met straal r. Deze n-hoek bestaat uit n gelijkbenige driehoeken met basis k, hoogte h en tophoek \beta. De oppervlakte van één zo'n driehoek is \eqalign{ O_{driehoek} = \frac{1} {2} \cdot k \cdot h}
Je krijgt dan:
\eqalign{ & h = r \cdot \cos \left( {\frac{\beta } {2}} \right) \cr & k = 2 \cdot r \cdot \sin \left( {\frac{\beta } {2}} \right) \cr}
Invullen geeft:
\eqalign{ & O_{driehoek} = \frac{1} {2} \cdot k \cdot h \cr & O_{driehoek} = \frac{1} {2} \cdot 2 \cdot r \cdot \sin \left( {\frac{\beta } {2}} \right) \cdot r \cdot \cos \left( {\frac{\beta } {2}} \right) \cr & O_{driehoek} = r^2 \cdot \sin \left( {\frac{\beta } {2}} \right) \cdot \cos \left( {\frac{\beta } {2}} \right) \cr & O_{driehoek} = \frac{1} {2} \cdot r^2 \cdot \sin \left( \beta \right) \cr}
Voor de oppervlakte van de regelmatige n-hoek kan je op dezelfde manier de formule voor een willekeurige waarde van n afleiden:
\eqalign{ & O_{n - hoek} = \frac{1} {2} \cdot n \cdot r^2 \cdot \sin \left( \beta \right) \cr & \beta = \frac{{360^\circ }} {n} \cr}
Oftewel:
\eqalign{O_{n - hoek} = \frac{1} {2} \cdot n \cdot r^2 \cdot \sin \left( {\frac{{360^\circ }} {n}} \right)}
Daarmee kan je voor een regelmatige n-hoek de oppervlakte uitrekenen.
Als je de hoeken liever in radialen wilt uitdrukken dan krijg je:
\eqalign{O_{n - hoek} = \frac{1} {2} \cdot n \cdot r^2 \cdot \sin \left( {\frac{{2\pi }} {n}} \right)}
Voor r=1 en n\to\infty zou hier dan \pi uit moeten komen...

Naschrift
Dit kan ook:
\eqalign{O_{n - hoek} = n \cdot r^2 \cdot \sin \left( {\frac{\pi } {n}} \right)\cos \left( {\frac{\pi } {n}} \right)}
Dat is ook leuk...

WvR
3-2-2002