$$\int\frac1{x\sqrt{x^2+x+1}}\,\mathrm{d}x
$$De eerste stap is kwadraat afsplitsen in $x^2+x+1$; dat wordt $\eqalign{(x+\frac12)^2+\frac34}$.
Vervang $\eqalign{x+\frac12}$ door $y$:
$$\int\frac1{(y-\frac12)\sqrt{y^2+\frac34}}\,\mathrm{d}y
$$Je kunt de wortel iets mooier maken door $\eqalign{y=\frac{\sqrt3}{2}z}$ te nemen: dan $\eqalign{y^2+\frac34=\frac34z^2+\frac34=\frac34(z^2+1)}$; er komt
$$\int\frac1{\frac{z\sqrt3-1}2\cdot\frac{\sqrt3}2\cdot\sqrt{z^2+1}}
\frac{\sqrt3}2\,\mathrm{d}z
=\int\frac2{z\sqrt3-1}\cdot\frac1{\sqrt{z^2+1}}\,\mathrm{d}z
$$Nu bekijken we deze driehoek:
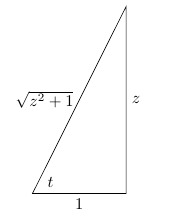
We substitueren $z=\tan t$.
Dan krijgen we ook $\eqalign{\frac1{\sqrt{z^2+1}}=\cos t}$ en $\eqalign{\mathrm{d}z=\frac1{\cos^2t}\,\mathrm{d}t}$.
Er komt
$$\int\frac2{\sqrt3\tan t-1}\cdot\cos t\cdot\frac1{\cos^2t}\,\mathrm{d}t
=\int\frac2{\sqrt3\sin t-\cos t}\,\mathrm{d}t
$$Voor dit soort integralen is $u=\tan\frac12t$ een veelgebruikte substitutie.
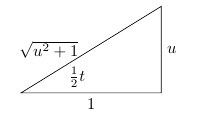
Nu krijgen we $\eqalign{\sin\frac12t=\frac u{\sqrt{u^2+1}}}$ en $\eqalign{\cos\frac12t=\frac1{\sqrt{u^2+1}}}$ en door de verdubbelingsformules vinden we
$$\sin t=\frac{2u}{u^2+1},\qquad
\cos t=\frac{1-u^2}{1+u^2}, \quad\text{ en }\quad
\tan t=\frac{2u}{1-u^2}
$$Met $t=2\arctan u$ komt er uiteindelijk
$$\int \frac2{\frac{2\sqrt3u}{1+u^2}-\frac{1-u^2}{1+u^2}}\cdot
\frac2{1+u^2}\,\mathrm{d}u=
\int \frac4{u^2+2\sqrt3u-1}\,\mathrm{d}u
$$De noemer kunnen we ontbinden als $(u+\sqrt3-2)(u+\sqrt3+2)$ en daarmee kunnen we de integraal schrijven als:
$$\int \frac1{u+\sqrt3-2}-\frac1{u+\sqrt3+2}\,\mathrm{d}u
$$De primitieve wordt dus
$$\ln(u+\sqrt3-2)-\ln(u+\sqrt3+2)
$$of
$$\ln\left(\frac{u+\sqrt3-2}{u+\sqrt3+2}\right)
$$Nu terugwerken.
Merk op dat we hebben gezien dat $\eqalign{z=\tan t=\frac{2u}{1-u^2}}$, hiermee kunnen we $u$ in $z$ uitdrukken: we lossen
$$zu^2+2u-z=0 \text{ of } u^2+\frac2zu-1=0
$$op: kwadraat afsplitsen geeft
$$\left(u+\frac1z\right)^2-\frac{z^2+1}{z^2}=0
$$en dus
$$u=-\frac1z\pm\frac1z\sqrt{z^2+1}
$$Omdat $u$ en $z$ hetzelfde teken moeten hebben nemen we
$$u=\frac1z\bigl(\sqrt{z^2+1}-1\bigr)
$$Nu nog netjes $\eqalign{z=\frac2{\sqrt3}(x+\frac12)}$ invullen en uitwerken.
NB we hadden de substituties $z=\tan t$ en $u=\tan\frac12t$ in een keer kunnen doen, met behulp van $\eqalign{z=\frac{2u}{1-u^2}}$ en $\eqalign{u=\frac1z\bigl(\sqrt{z^2+1}-1\bigr)}$, maar dat is wat onoverzichtelijker. Het zou wel een goede oefening in netjes werken zijn.
kphart
4-4-2022