WisFaq!

Bewijzen van de kwadratuur van een rechthoek

Ik heb genoeg informatie over hoe je een vierkant met hetzelfde oppervlakte kan maken vanuit een gegeven rechthoek. Alleen ik kan nergens informatie vinden (niet al te ingewikkeld ) waar het bewezen word dat de oppervlaktes daadwerkelijk gelijk zijn. Weet u misschien een site waar dit in niet al te langdradige/moeilijke uitleg staat? BvD

Erwin
2-4-2003

Antwoord

Eerst naar even naar de tekening kijken: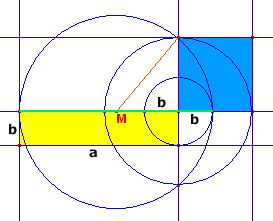



We zien een rechthoek met zijden a en b.
Te bewijzen: de zijde van het vierkant is √ab.

De straal van de cirkel met middelpunt M is (a+b)/2 (ga maar na!).
Het stukje rechts van M (tot het middelpunt van de kleine cirkel) heeft de lengte a+b-(a+b)/2-b=(a-b)/2 (ga maar na!).
En dan ben je er al bijna:



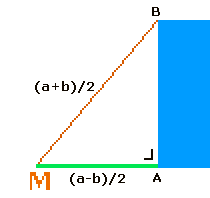
Met de steling van Pythagoras in $\Delta$MAB kan je lengte van AB berekenen en als het goed is kom je uit op √(ab).

Zie ook Bewijs voor de kwadratuur van de rechthoek.

WvR
2-4-2003