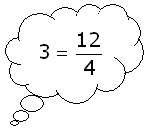WisFaq!

Tijdsduur berekenen met afstand en snelheid

Oscar en Paul zijn met de auto een weekend naar Parijs geweest. Op de heenweg legden ze 520 km in 5 uur af. Tot de tussenstop reden ze gemiddeld 120 km per uur. Na de tussenstop hadden ze veel pech met files. Dit stuk reden ze met een gemiddeld snelheid van 80 km per uur.

• Stel een vergelijking op en bereken hiermee de tijd die Oscar en Paul voor het tweede gedeelte nodig hebben gehad.

Muhammed Talha Erdemsoy
15-12-2021

Antwoord

Gebruik de formule:

$\eqalign{v=\frac{S}{t}}$ met:

$v$: gemiddelde snelheid in km/uur
$S$: afgelegde weg in km
$t$: tijd in uur

Als ze over het eerste stuk $t$ uur doen dan doen ze over het tweede stuk $5-t$ uur. Als het eerste stuk $S$ km is dan is het tweede stuk $520-S$ km. Er geldt:

Nu geldt $
\eqalign{\frac{S}
{t} = 120}
$ en $
\eqalign{\frac{{520 - S}}
{{5 - t}} = 80}
$.

Oftewel:

$
\eqalign{
& S = 120t \cr
& 520 - S = 80(5 - t) \cr}
$

Je kunt nu $
S = 120t
$ invullen in de tweede vergelijking. Je krijgt dan:

$
\eqalign{
& 520 - S = 80(5 - t) \cr
& 520 - 120t = 400 - 80t \cr}
$

Kan je de vergelijking oplosssen? Je weet dan $t$. Hoe lang doen ze dan over het tweede stuk? Lukt dat zo?

WvR
15-12-2021