WisFaq!

Re: Lim sin(x)/x berekenen met eenheidscirkel

Ik heb altijd geleerd dat het teken omklapt als je beide zijden van een vergelijking vermenigvuldigt met -1.

In mijn oude wiskunde boek staat bij de uitleg:

Ga maar na:

1 $<$ 1¹/₂ $<$ 2 $
\Leftrightarrow
$ 1 $>$ ²/₃ $>$ ¹/₂.

Mag je zo'n truc zomaar toepassen op goniometrische functies?
Ik heb bovenstaande trucs nooit geleerd op school.
Wordt dit in bepaalde lesstof behandeld?

Peter Schilder
15-11-2021

Antwoord

Hallo Peter,

Wat jij beschrijft is niet vermenigvuldigen met -1 (dan klapt het teken overigens ook om), maar tot de macht -1 verheffen, oftewel het omgekeerde nemen.

In het voorbeeld dat je geeft en in de berekening die je aanhaalt kun je die truc inderdaad gebruiken. Dat heeft te maken met het feit dat de "omkering", de grafiek van $y=1/x=x^{-1}$, dalend is. Dus als je x groter neemt, wordt y kleiner. Althans ...



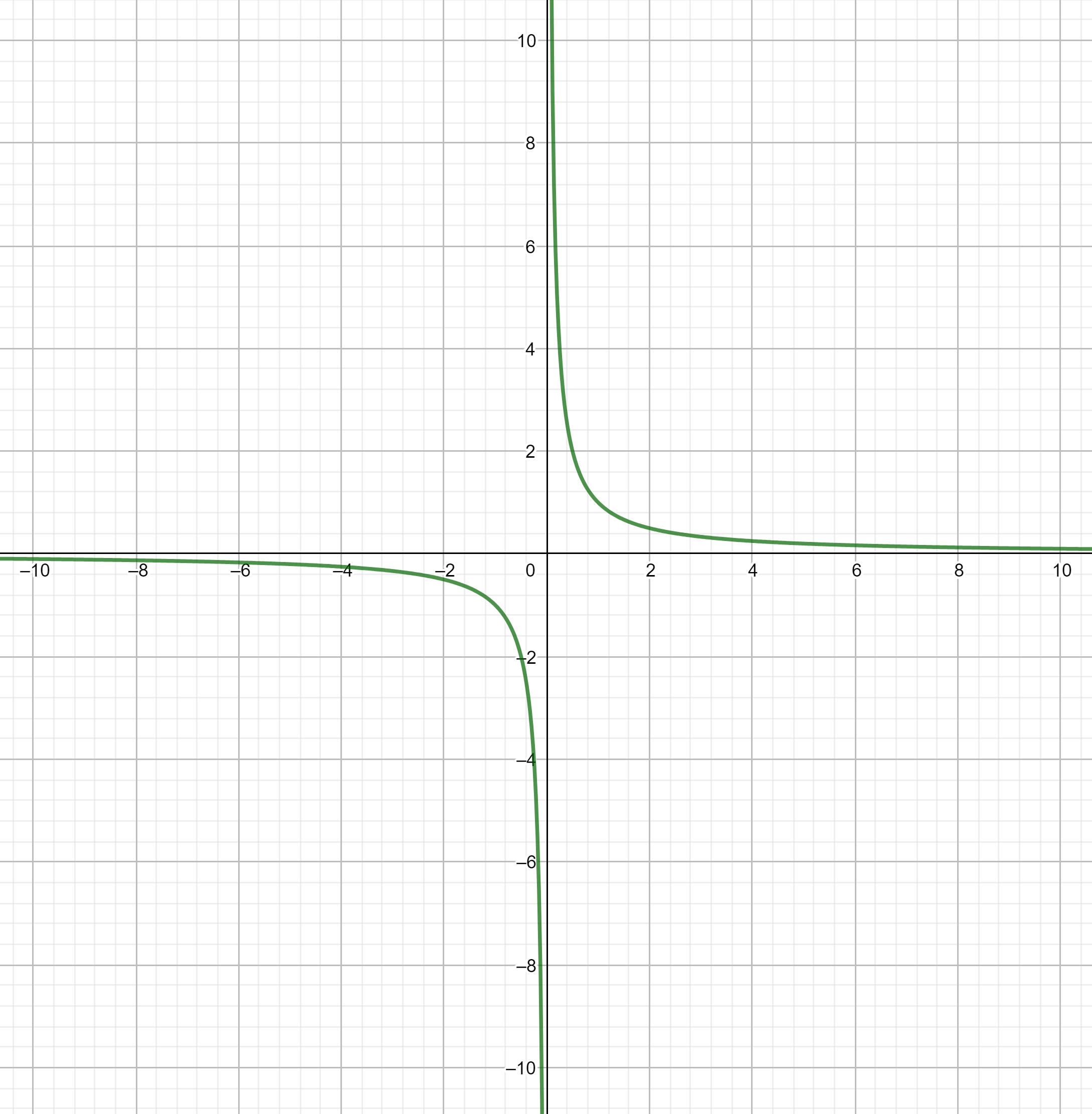
Zoals je ziet zit er een sprong in de grafiek. Van de negatieve naar de positieve kant op de horizontale as ($x$-as), springt de grafiek van onder naar boven, zeg van min oneindig naar plus oneindig. En daalt daarna weer verder.

De truc werkt dus alleen als de getallen in de ongelijkheid allemaal negatief of allemaal positief zijn. Dus als dat zo is, mag je de truc gewoon toepassen, ook als er goniometrische functies in het spel zijn.

Zover ik weet wordt dit niet op middelbare scholen uitgelegd, maar helemaal zeker weet ik dat niet.

Met vriendelijke groet,

FvL
15-11-2021