WisFaq!

Regelmatige vijfhoek

Hoi,
Ik hoop dat u me kunt helpen met deze opgave....
ABCDE is een regelmatige vijhoek en C(0,r) is zijn omgeschreven cirkel. M een punt op de kleine boog [AB].
H1, H2, H3, H4, H5 zijn de afstanden tussen het punt M en de lijnen (AB), (BC), (CD), (DE) en (EA)

toon aan:
H2+ H3+ H4+ H5-H1= (2·S)/c
waarbij S is de oppervlakte ABCDE en c de lengte van AB
alvast bedankt

asmar
1-4-2003

Antwoord

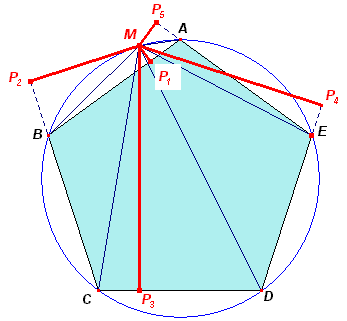
In bovenstaande figuur zijn de lijnstukken MP1, MP2, ... de bedoelde afstanden H1, H2, ... van M tot de zijden van de vijfhoek.
Die afstanden kunnen dienen als hoogte van de driehoeken MAB, MBC, MCD, MDE en MEA.
Laten we de oppervlaktes van die driehoeken, opvolgend O1, O2, O3, O4, O5 genoemd, eens bekijken.
Dan zien we dat voor de oppervlakte S van de vijfhoek geldt:
S = O2 + O3 + O4 + O5 - O1
Nu is bijvoorbeeld O2 = ¹/₂·H2·c (etc).
Dan is het denk ik nu niet moeilijk meer de formule verder zelf af te leiden.

dk
1-4-2003