WisFaq!

Re: Kegelsneden

De formules zijn van een

• parabool: y² = 4ax
• ellips: (x²/a²) + (y²/b²) = 1
• hyperbool (x²/a²) - (y²/b²) = 1
• cirkel x² + y² = R²

Zou u hier voorbeelden van kunnen geven die algebraïsch zijn opgelost?
Alvast vriendelijk bedankt.

Flo
31-3-2003

Antwoord

Parabool
Hieronder staan een aantal voorbeelden van dit 'soort' parabolen:



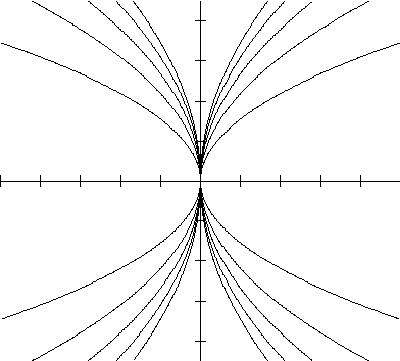
Hierbij 'loopt' a van -3 tot 3.

Neem aan dat de parabool door (3,6) loopt, dan kan je de waarde van a uitrekenen (a is immers de parameter die je kan kiezen):
6²=4a·3
36=12a
a=3
Dus de parabool y²=12x gaat door het punt (3,6).

Ellips
Bij deze formule heb je twee parameter, a en b. Dat betekent dat de ellips pas vastligt bij 2 punten.

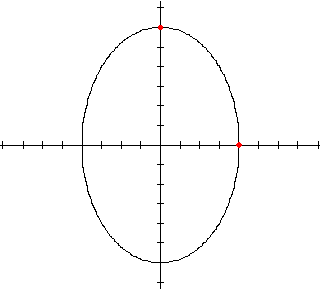
We nemen een paar handige punten: (4,0) en (0,6)
Eerst (4,0) invullen:
4²/a²=1
a²=16
a=4 (of a=-4)

(0,6) invullen:
0²/(1/16)+6²/b²=1
36/b²=1
b²=36
b=6 (of b=-6)

Dus x²/4²+y²/6²=1 gaat door (4,0) en (0,6).




Hyperbool
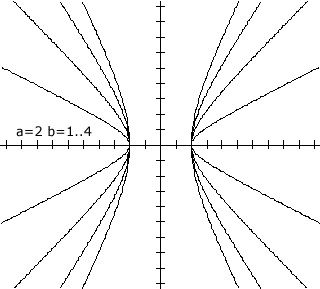
Dit lijkt op het verhaal bij de ellips, maar dan anders... Hieronder zie je een paar voorbeelden van dit soort hyperbolen: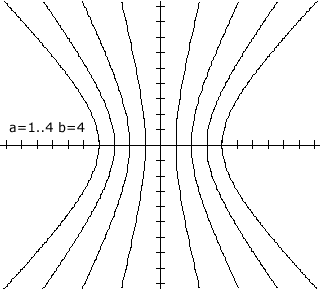






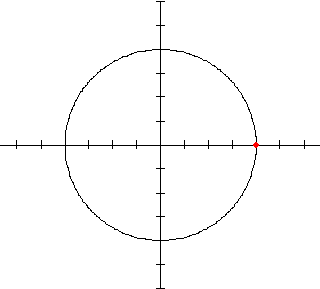
Cirkel
Ook hier heb je weer te maken met één parameter, namelijk de straal R. Dus bijvoorbeeld zo'n cirkel door het punt (4,0):
4²+0²=r²
16=r²
r=4
De cirkel met straal 4 gaat door (4,0).




Hopelijk helpt dit. Het zou helpen als je zelf concrete vraagstukken zou sturen. Dit blijft toch een beetje vaag!

WvR
1-4-2003