WisFaq!

Integreren goniometrische veelterm

Goede avond,

Gegeven:

I=((4-cos²x+2cosx-sinx))dx/(2+cosx)²

Substutie geprobeerd, ook splitsing van termen.Ik geraak niet vertrokken.Vilgensd wxolfram is het een moeilijk en lang eindresultaat....
Enkele hints zouden welkom zijn.
Groeten

Rik Lemmens
5-5-2021

Antwoord

Een standaardsubstitutie in dit geval is $u=\tan\frac x2$, ofwel $x=2\arctan u$.
Dan verandert $dx$ in $\frac2{1+u^2}\,du$.
Verder geldt natuurlijk $\cos x=\cos^2\frac x2-\sin^2\frac x2$, en $\sin x=2\sin\frac x2\,\cos\frac x2$.
Hoe helpt dit?

Welnu, bekijk dit plaatje

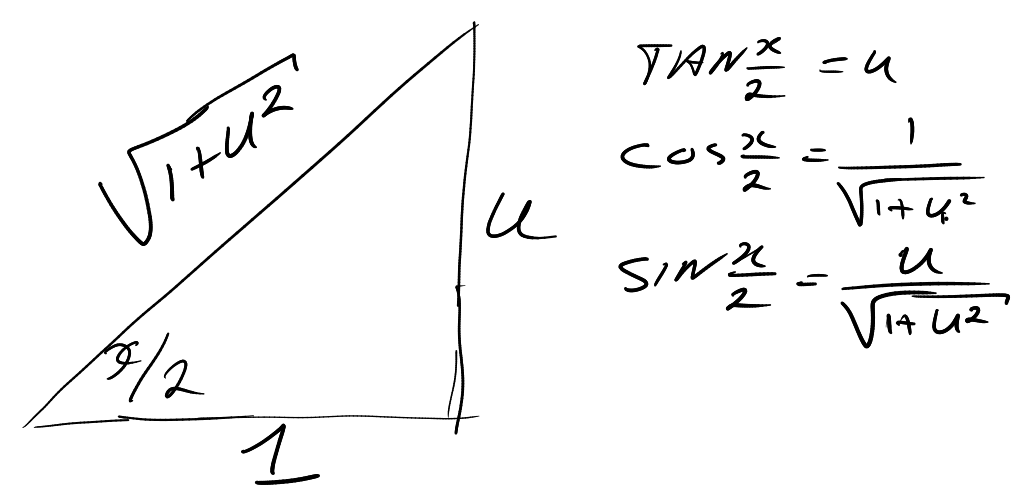
Nu volgt
$$\cos x= \frac{1-u^2}{1+u^2}\text{ en }\sin x=\frac{2u}{1+u^2}
$$Als je dit netjes invult en uitwerkt krijg je een quotiënt van twee polynomen dat je met behulp van breuksplitsen etc kunt primitiveren, waarna invullen van $u=\tan\frac x2$ de gewenste primitieve oplevert.

kphart
5-5-2021