WisFaq!

Re: Fietsketting

veronderstel nu dat de fietskettingen 99 schakels hebben en dat je sigma kan aanpassen. welke waarde voor sigma zorgt ervoor dat minstens 90% van alle fietskettingen voldoen aan de voorwaarde?

hoe moet ik dit doen? sigma zou $\le$ 0,03055 cm moeten zijn. maar ik weet niet hoe je die vergelijking moet opstellen.

elke
3-4-2021

Antwoord

Hallo Elke,

De vraag komt er dus op neer:

• De lengte van de fietsketting is normaal verdeeld,
  
• De gemiddelde lengte is 99·0,5=49,5 cm
  
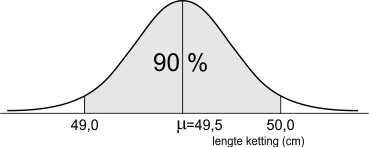
• Hoe groot moet $\sigma$ zijn zodat 90% van de lengtes tussen 49 en 50 cm ligt?

Maak voor dit soort vragen een schets van de normaalverdeling, dat helpt om inzicht in het probleem te krijgen. In dit geval ziet de schets er zo uit:



Het vervolg hangt af van de hulpmiddelen die je gebruikt. Je kunt deze normaalverdeling omrekenen naar een standaardnormale verdeling en vervolgens een tabel of op je grafische rekenmachine de functie InvNorm gebruiken om een z-waarde te bepalen. Deze z-waarde reken je weer om naar de standaardafwijking (zie het laatste voorbeeld op pagina 8 en opgave 3.2 van de lesbrief waarnaar eerder is verwezen.
Op je grafische rekenmachine kan je ook twee formules invoeren:

y1=normalcdf(ondergrens=49, bovengrens=50, $\mu$=49.5, $\sigma$=X)
y2=0,9

en vervolgens het snijpunt van de grafieken bepalen. Je rekenmachine zoekt dan de waarde van X (dus: van $\sigma$) waarvoor de oppervlakte tussen l=49 en l=50 gelijk is aan 0,9.

Let op: Wanneer je op deze wijze een standaardafwijking hebt berekend, dan is dit de standaardafwijking van de lengte van de ketting ($\sigma$_ketting), dus van de som van 99 lengtes van afzonderlijke schakels. De vraag is om de standaardafwijking te berekenen van de lengte van afzonderlijke schakels ($\sigma$_schakel). Het verband tussen deze standaardafwijkingen wordt gegeven door de wortel-n-wet:

$\sigma$_ketting = (√n)·$\sigma$_schakel

Je moet je gevonden waarde voor $\sigma$_ketting dus nog wel delen door √99 0m de gevraagde $\sigma$_schakel te vinden.

GHvD
4-4-2021