WisFaq!

Re: Enquete

dankuwel!! ik heb een ander vraag als volgt: hoe groot moet de steekproefgrootte zijn om de standaardafwijking van P^terug te brengen tot 0,5%? wat betekent dit in het licht van de 68-95-99,7% vuistregel?

ik snap niet echt hoe ik n moet vinden en waar die regel ermee te maken heeft?

een ander vraag; Ik wijk bij het berekenen van mijn uitkomsten vaak af van de modeloplossing, is dit iets ergs of is het normaal? vaak verschilt dit met 0,001 of 0,002 en soms met 0,01 wel. ik weet niet of dit dan is door afrondingen of misschien dat er gebruik wordt gemaakt van een tabel maar ik wijk soms wel af.

elke
3-4-2021

Antwoord

Hallo Elke,

In het antwoord op jouw vorige vraag gaf ik al aan dat voor de standaarddeviatie geldt:



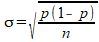
Wanneer je bij $\widehat p$=0,49 eist dat $\sigma$=0,005, dan moet kennelijk gelden:



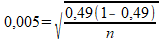
De vereiste grootte van de steekproef (dus: n) vind je door deze vergelijking op te lossen. Gaat dat lukken?

Wat betreft de betekenis van de vuistregels:
Bij een normaalverdeling ligt 68% van de waarnemingen binnen één keer de standaardafwijking van het gemiddelde, 95% van de waarnemingen binnen twee keer de standaardafwijking en 99,7% binnen drie keer de standaardafwijking van het gemiddelde. Met $\sigma$=0,005 betekent dit:
Met 68% betrouwbaarheid is de foutenmarge 0,005 (dus: +/- 0,5%);
Met 95% betrouwbaarheid is de foutenmarge 0,01 (dus: +/- 1%);
Met 99,7% betrouwbaarheid is de foutenmarge 0,015 (dus: +/- 1,5%);

Wat betreft de verschillen tussen jouw antwoorden en modelantwoorden: in het algemeen kan ik natuurlijk niet aangeven waar dit aan ligt. Zeker als door jou of voor het modelantwoord tabellen worden gebruikt, kunnen afrondingsfouten een rol spelen. Immers, je kunt geen tabel maken met oneindig veel waarden. Vaak moet je aflezen bij een waarde die het dichts ligt bij de waarden uit de opgave. Hierbij wordt dan een afrondfout gemaakt.

GHvD
4-4-2021