WisFaq!

Sinus- en cosinusregel

Goeiemorgen!
Ik heb eigenlijk nog enkele vraagjes.

1. Toon aan dat in elke driehoek ABC geldt:
bc.cos$\alpha$ + ac.cos$\beta$+ ab.cos$\gamma$ = ¹/₂ (a²+b²+c²)

2. De deellijn van een hoek van een driehoek verdeelt de overstaande zijde in twee lijnstukken die zich verhouden als de aanliggende zijden.

3. Bewijs: in driehoek ABC geldt: a = b.cos$\gamma$ + c.cos$\beta$.

4.
a. Teken in een cirkel c(O,3cm) de koorde [BC] zo dat BC = 4,5cm.
b. Teken met [BC] als basis de gelijkbenige driehoeken zo dat c(O,3cm) de omgeschreven cirkel is van de driehoeken.
c. Los de driehoeken op.

Als je me gewoon even enkele tips kunt geven ben ik al heel tevreden!
Bedankt!

M.
30-3-2003

Antwoord

Je vraagt om tips. Daar komen ze.

1. Schrijf de cosinusregel eens op voor elk van de drie zijden van de driehoek.
Tel de linker leden en de rechter leden van die uitdrukkingen eens bij elkaar op.

2. Over de deellijn van een hoek (had je die vraag al niet eens eerder gesteld?).
Teken de deellijn uit hoek A die BC snijdt in D. Kies op de deellijn een punt S zodat BS = AB.
Kijk dan eens naar de driehoeken BSD en CAD (zijn die soms gelijkvormig?)

3. Het bewijs van a = b.cos(C) + c.cos(B)
Teken de hoogtelijn AD. Bereken cos(B) in driehoek ABD.
En bereken ook CD in driehoek ...

4. Met het "oplossen van de driehoek" bedoel je denk ik het berekenen van de zijden en de hoeken.
Je hebt natuurlijk al een tekening gemaakt. En daarin is wel het een en ander te zien.



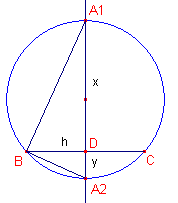
Waarom is A₁BA₂ = 90°?
Zij A₁D = x, A₂D = y en BD = h (h heeft een bekende waarde).
Dan is:
h² = xy (toch?)
en
x + y = ...
Hieruit kan je x en y berekenen.
En de Stelling van Pythagoras brengt je dan wel verder.

dk
30-3-2003