WisFaq!

De recurrente betrekking

Dag heer/mevrouw,

Ik kom bij deze opgave niet uit.

Zij gegeven de rij a₀; a₁; a₂; ..... die als volgt met recursie is gedefinieerd:

• a₀ = 4, a₁ = 18
• a_n+2 = 5a_n+1 - 6a_n voor alle n $\ge$ 0.

Gevraagd:

1. Bereken a₁₀ met behulp van de recurrente betrekking (gebruik de SEQ-modus van je GR, met de uitleg van de stappen).
2. Geef een directe formule voor a_n met behulp van de lineaire recurrente betrekkingen.
3. Bereken nogmaals a₁₀, maar nu met de directe formule.

Pet
23-2-2021

Antwoord

1.

De 1e vraag is wel een beetje lastig. Ik heb een TI-84 Plus CE-T gebruikt. Je moet maar 's goed kijken naar de instellingen. Je hebt de volgende onderdelen nodig. Ik neem aan dat je daar mee voldoende uit de voeten kan:

[MODE]



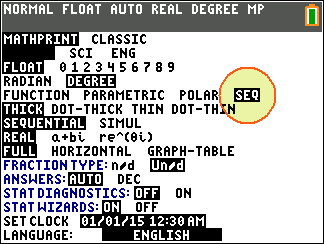
[y=]



[table]



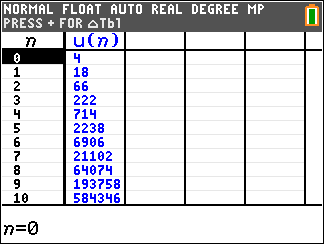
2.

Op lineaire differentievergelijkingen van de tweede orde staat uitgelegd hoe je een directe formule kan opstellen. Zie uitwerking voorbeeld 1.

3.

Ik kom dan uit op:

$
\eqalign{
& a_n = 10 \cdot 3^n - 6 \cdot 2^n \cr
& a_{10} = 10 \cdot 3^{10} - 6 \cdot 2^{10} = {\rm{584}}{\rm{.346}} \cr}
$

...en dan lijkt het me wel in orde zo. Zou dat lukken denk je?

WvR
23-2-2021