Een warenhuis wil een filiaal vestigen en koopt daarvoor een rechthoekig stuk grond. De oppervlakte van het rechthoekig warenhuis zelf zal 3125 m2 bedragen. Links en rechts wil men een 5 meter brede groenzone voorzien. Achter het warenhuis komt een rechthoekige strook open opslagruimte met een lengte van 20 meter. Voor het warenhuis voorziet men een rechthoekig parkeergebied met een lengte van 80 meter.
- Bepaal de afmetingen van het gebouw zodat het totale terrein een zo klein mogelijke oppervlakte heeft.
- Hoeveel m2 moet dan worden opgekocht?
satya
16-1-2021
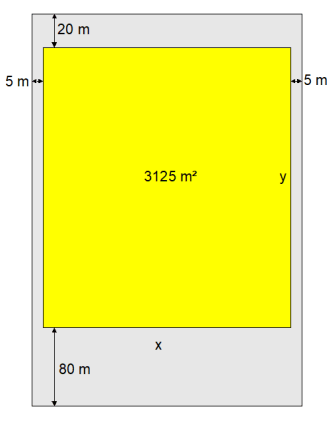
Voor het warenhuis geldt:
$
xy = 3125
$
Voor het terrein geldt:
$
O = (x + 10)(y + 100)
$
Je kunt daarmee de oppervlakte uitdrukken in $x$ en dan met behulp van de afgeleide bepalen voor welke waarde van $x$ de oppervlakte minimaal is. De rest zal dan ook wel gaan.
Zou dat lukken?
WvR
16-1-2021
#91372 - Differentiëren - Student Hoger Onderwijs België
