WisFaq!

Re: De manteloppervlakte van een omwentelingslichaam

Ik weet wel dat men het moet zien als de som van afgeknotte kegeltjes maar ik begrijp niet waarom de manteloppervlakte de integraal niet is van $2\pi·f(x)$. $f(x)$ is toch ook een kromme. Als je de inhoud van en omwentelingslichaam zoekt neemt men toch ook de integraal van $\pi·f(x)$ in het kwadraat

Eddy Raymaekers
24-11-2020

Antwoord

Dit volgt rechtstreeks uit de basisformules voor de afgeknotte kegel.

De inhoud is
¹/₃.$\pi$.h.(r₁²+r₁.r₂+r₂²)
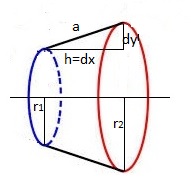
r₁ en r₂ worden gelijk aan f(x) voor kleine hoogtes h = dx
Dus wordt dit ¹/₃.$\pi$.3.f²(x).h =
$\pi$.f²(x).h = $\pi$.f²(x).dx

De manteloppervlakte is
$\pi$.(r₁ + r₂).a =
2.$\pi$.f(x).a
met a = √(d²x + d²y)
= √(1 + f^'2(x)).dx

Dus bij de inhoud van een afgeknotte kegel speelt de hoogte een rol, bij de manteloppervlakte speelt het apothema een rol.

LL
25-11-2020