WisFaq!

Koordenvierhoek

Hoe kan je nu bewijzen dat in een koordenvierhoek de overstaande hoekpunten supplementair zijn?

Ornelis Seba
27-3-2003

Antwoord

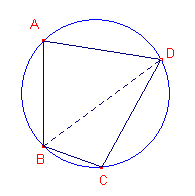
Ken je de stelling van de omtrekshoek?
Een omtrekshoek van een cirkel is gelijk aan de helft van de boog waarop hij staat.
Dus in bovenstaande figuur is:
ÐA = ¹/₂bg(BCD)
en ook
ÐC = ¹/₂bg(BAD)
Tellen we beide uitdrukkingen op dan vinden we:
ÐA + ÐC = ¹/₂(bg(BCD) + bg(BAD)) = ¹/₂.360^o = 180^o
De hoeken A en C zijn dus supplementair. En de hoeken B en D dus ook!

dk
27-3-2003