WisFaq!

Spiegeling parabool op een punt

Goede avond ,
Volgend probleem snap ik niet goed.....
Parabool p(2) is het beeld van de gegeven P(1) y=x² ten overstaan van het punt door spiegelen van Co(A)=(0,-2)
Zijn er voorbeelden te vinden op Wisfaq over deze problematiek. Kunnen jullie mij wat op weg zetten om , via een figuur e wat uitleg te laten zien dat het resultaat
y=-x²-4 moet zijn.
Vriendelijke groeten en een goede nacht

Rik Lemmens
8-10-2020

Antwoord

Je kunt op twee manieren (die bijna op hetzelfde neerkomen) aan de vergelijking komen.

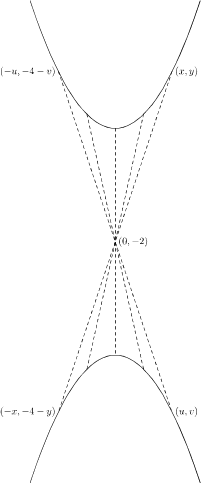
Neem een punt $(x,y)$ op de parabool, het beeldpunt is $(-x,-4-y)$; in die uitdrukking kunt je $-4-y$ vervangen door $-4-x^2=-4-(-x)^2$. Er staat dus $(-x,-4-(-x)^2)$. Daar staat het gegeven antwoord; je kunt de variabelen hernoemen: $-x=t$ geeft $(t,-t^2-4)$.

Andersom kan ook: neem een punt $(u,v)$ op de beeldkromme en kijk naar zijn origineel $(-u,-4-v)$; dar moet aan de vergelijking voldoen, dus moet gelden $-4-v=(-u)^2$, en dat kun je omwerken tot $v=-u^2-4$.

kphart
9-10-2020