WisFaq!

Constructie van een driehoek

Situatieschets: Construeer een driehoek ΔABC als gegeven is, ∠A en de deellijn d_a uit hoek A.

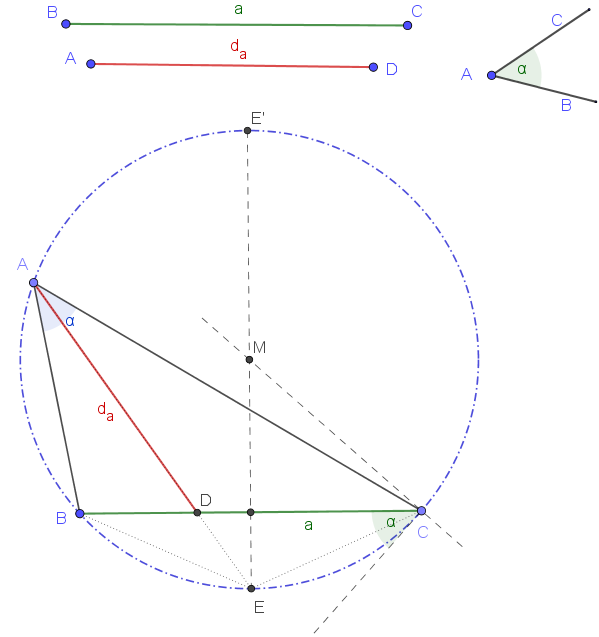
Mijn bevindingen: Zoals in bijgaande figuur is te zien, bepaalde ik de cirkelboog van waaruit men de zijde a onder de gegeven hoek ∠A kan zien. De middelloodlijn van BC snijdt de omgeschreven cirkel van ΔABC in E (zie figuur). Het is evident dat de bg(BE) bg(CE) alsook BE = CE. Het verlengde van de gezochte deellijn d_a uit A zal dus door E gaan. Om echter A te kunnen vastleggen zodanig dat d_a de opgegeven lengte heeft, dient men echter het punt D juist te lokaliseren op BC. Het is nu precies daar waar ik vast loop. Ik dacht o.a. aan de bissectricestelling, d_a² = AB.AC - BD.CD, aan de koordenvierhoek ABEC, een verhouding zoeken met een 4e evenredige, enz... wellicht zie ik hier iets over het hoofd.

Ik kwam er wel achter dat er maximaal 2 oplossingen kunnen zijn, soms maar één en als d_a $>$ a/2 · cotg(∠A/2) is er zelfs geen oplossing.

VRAAG: Graag had ik een tip gekregen om de juiste positie van het punt D gelegen op BC vast te leggen. Mijn oprechte dank voor jullie tussenkomst!

Yves De Racker
3-8-2020

Antwoord

Hallo Yves,

Niet bepaald de makkelijkste constructie. Onderstaande constructie met uitleg (in het Engels) zou je verder moeten helpen. Let op: stap 2 van de constructie moet worden toegepast op cirkel (D) uit stap 3.

Succes!

Met vriendelijke groet,

Zie Construction of Triangle from Side, Angle, and that Angle's Bisector [https://www.cut-the-knot.org/triangle/SideAngleAngleBisector.shtml]

FvL
3-8-2020