WisFaq!

Oppervlakte tussen twee krommen

Goede avond,

y²=4x en y=3-x. De ene stel ik f en de andere g. Ik ben al een tijd aan het rekenen geweest maar kan de oplossing 64/3 niet vinden. Ik denk dat ik iets verkeerd doe in de opeenvolgende vakjes waar gebied ligt tussen de twee krommen. Graag wat hulp als het kan.Graag een figuur daarbij als het mogelijk is (parabool die een rechte snijdt.

Groeten

RIK LEMMENS-
30-5-2020

Antwoord

Als het gaat om de oppervlakte van het gebied tussen f en g dan hoort daar waarschijnlijk dit plaatje bij:



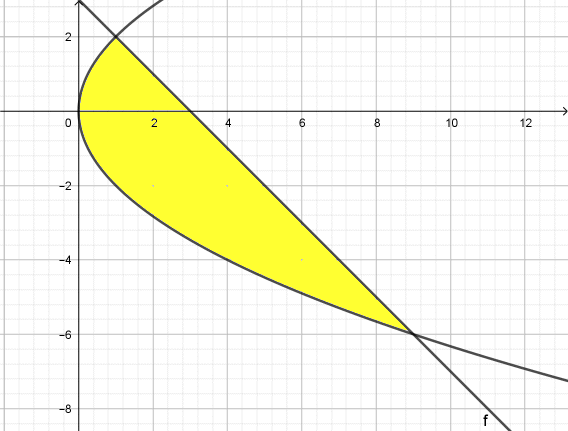
Maar dan is het handiger om te integreren via de y-as. Je kan er dit plaatje van maken:



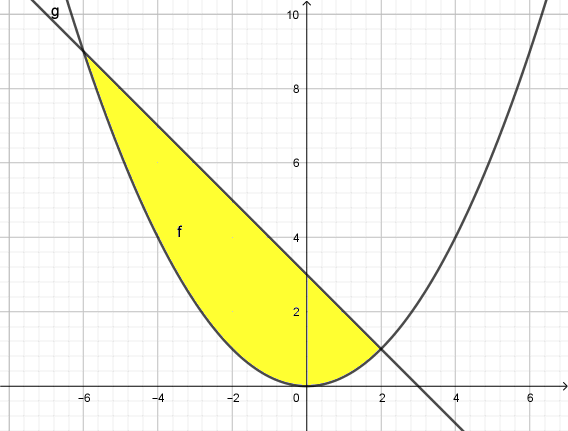
Met:

$
\eqalign{
& f:y = {{x^2 } \over 4} \cr
& g:y = 3 - x \cr}
$

Er komt voor de integraal en de oppervlakte $
\eqalign{{{64} \over 3}}
$ uit. Zou dat lukken?

WvR
30-5-2020